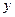二、填空題,本大題共7小題,考生作答6小題.每小題5分共30分,把答案填在答題卡中對應題號后的橫線上.
(一)選做題,(請考生在第10,,1兩題中任選一題作答,如果全做 ,則按前一題記分)
10.在極坐標系中,曲線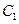 :
: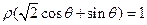 與曲線
與曲線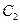 :
: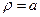
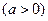 的一個交點在極軸上,則a=_______.
的一個交點在極軸上,則a=_______.
【答案】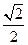
【解析】曲線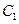 的直角坐標方程是
的直角坐標方程是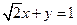 ,曲線
,曲線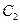 的普通方程是直角坐標方程
的普通方程是直角坐標方程
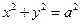 ,因為曲線C1:
,因為曲線C1: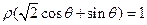 與曲線C2:
與曲線C2: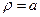
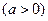 的一個交點在極軸上,所以
的一個交點在極軸上,所以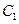 與
與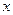 軸交點橫坐標與
軸交點橫坐標與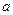 值相等,由
值相等,由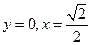 ,知
,知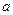 =
=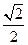 .
.
【點評】本題考查直線的極坐標方程、圓的極坐標方程,直線與圓的位置關系,考查轉化的思想、方程的思想,考查運算能力;題型年年有,難度適中.把曲線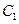 與曲線
與曲線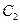 的極坐標方程都轉化為直角坐標方程,求出與
的極坐標方程都轉化為直角坐標方程,求出與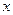 軸交點,即得.
軸交點,即得.
11.某制藥企業為了對某種藥用液體進行生物測定,需要優選培養溫度,實驗范圍定為29℃~63℃.精確度要求±1℃.用分數法進行優選時,能保證找到最佳培養溫度需要最少實驗次數為_______.
【答案】7
【解析】用分數法計算知要最少實驗次數為7.
【點評】本題考查優選法中的分數法,考查基本運算能力.
(二)必做題(12~16題)
12.不等式x2-5x+6≤0的解集為______.
【答案】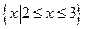
【解析】由x2-5x+6≤0,得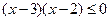 ,從而的不等式x2-5x+6≤0的解集為
,從而的不等式x2-5x+6≤0的解集為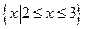 .
.
【點評】本題考查一元二次不等式的解法,考查簡單的運算能力.
13.圖2是某學校一名籃球運動員在五場比賽中所得分數的莖葉圖,則該運動員在這五場比賽中得分的方差為_________.
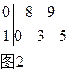
(注:方差
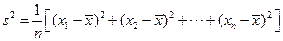 ,其中
,其中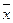 為x1,x2,…,xn的平均數)【答案】6.8
為x1,x2,…,xn的平均數)【答案】6.8
【解析】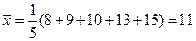 ,
,
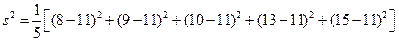
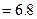 .
.
【點評】本題考查統計中的莖葉圖方差等基礎知識,考查分析問題、解決問題的能力.
14.如果執行如圖3所示的程序框圖,輸入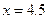 ,則輸出的數
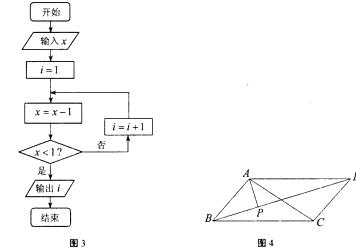
,則輸出的數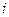 = .
= .
【答案】4
【解析】算法的功能是賦值,通過四次賦值得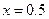 ,輸出
,輸出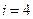 .
.
【點評】本題考查算法流程圖,考查分析問題解決問題的能力,平時學習時注意對分析問題能力的培養.
15.如圖4,在平行四邊形ABCD中 ,AP⊥BD,垂足為P,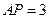 且
且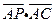 = .
= .
【答案】18
【解析】設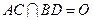 ,則
,則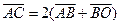 ,
,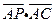 =
=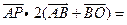
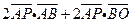
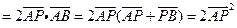
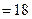 .
.
【點評】本題考查平面向量加法的幾何運算、平面向量的數量積運算,考查數形結合思想、等價轉化思想等數學思想方法.
16.對于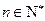 ,將n表示為
,將n表示為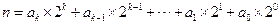 ,當
,當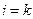 時
時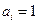 ,當
,當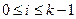 時
時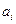 為0或1,定義
為0或1,定義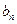 如下:在
如下:在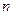 的上述表示中,當
的上述表示中,當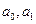 ,a2,…,ak中等于1的個數為奇數時,bn=1;否則bn=0.
,a2,…,ak中等于1的個數為奇數時,bn=1;否則bn=0.
(1)b2+b4+b6+b8=__;
(2)記cm為數列{bn}中第m個為0的項與第m+1個為0的項之間的項數,則cm的最大值是___.
【答案】(1)3;(2)2.
【解析】(1)觀察知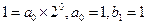 ;
;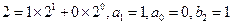 ;
;
一次類推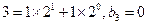 ;
;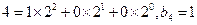 ;
;
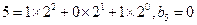 ;
;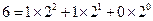 ,
,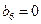 ,
,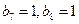 ,
,
b2+b4+b6+b8=3;(2)由(1)知cm的最大值為2.
【點評】本題考查在新環境下的創新意識,考查運算能力,考查創造性解決問題的能力.
需要在學習中培養自己動腦的習慣,才可順利解決此類問題.
三、解答題:本大題共6小題,共75分.解答應寫出文字說明、證明過程或演算步驟.
17.(本小題滿分12分)
某超市為了解顧客的購物量及結算時間等信息,安排一名員工隨機收集了在該超市購物的100位顧客的相關數據,如下表所示.
一次購物量 | 1至4件 | 5至8件 | 9至12件 | 13至16件 | 17件及以上 |
顧客數(人) |
| 30 | 25 |
| 10 |
結算時間(分鐘/人) | 1 | 1.5 | 2 | 2.5 | 3 |
已知這100位顧客中的一次購物量超過8件的顧客占55%.
(Ⅰ)確定x,y的值,并估計顧客一次購物的結算時間的平均值;
(Ⅱ)求一位顧客一次購物的結算時間不超過2分鐘的概率.(將頻率視為概率)
【解析】(Ⅰ)由已知得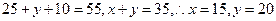 ,該超市所有顧客一次購物的結算時間組成一個總體,所收集的100位顧客一次購物的結算時間可視為一個容量為100的簡單隨機樣本,顧客一次購物的結算時間的平均值可用樣本平均數估計,其估計值為:
,該超市所有顧客一次購物的結算時間組成一個總體,所收集的100位顧客一次購物的結算時間可視為一個容量為100的簡單隨機樣本,顧客一次購物的結算時間的平均值可用樣本平均數估計,其估計值為:
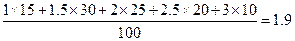 (分鐘).
(分鐘).
(Ⅱ)記A為事件“一位顧客一次購物的結算時間不超過2分鐘”,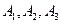 分別表示事件“該顧客一次購物的結算時間為1分鐘”, “該顧客一次購物的結算時間為
分別表示事件“該顧客一次購物的結算時間為1分鐘”, “該顧客一次購物的結算時間為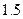 分鐘”, “該顧客一次購物的結算時間為2分鐘”.將頻率視為概率,得
分鐘”, “該顧客一次購物的結算時間為2分鐘”.將頻率視為概率,得
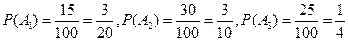 .
.
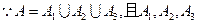 是互斥事件,
是互斥事件,
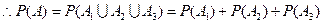
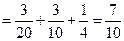 .
.
故一位顧客一次購物的結算時間不超過2分鐘的概率為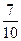 .
.
【點評】本題考查概率統計的基礎知識,考查運算能力、分析問題能力.第一問中根據統計表和100位顧客中的一次購物量超過8件的顧客占55%,知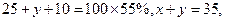 從而解得
從而解得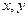 ,再用樣本估計總體,得出顧客一次購物的結算時間的平均值的估計值;第二問,通過設事件,判斷事件之間互斥關系,從而求得
,再用樣本估計總體,得出顧客一次購物的結算時間的平均值的估計值;第二問,通過設事件,判斷事件之間互斥關系,從而求得
一位顧客一次購物的結算時間不超過2分鐘的概率.
18.(本小題滿分12分)
已知函數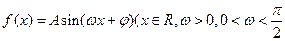 的部分圖像如圖5所示.
的部分圖像如圖5所示.
(Ⅰ)求函數f(x)的解析式;
(Ⅱ)求函數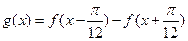 的單調遞增區間.
的單調遞增區間.
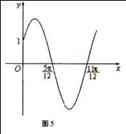
【解析】(Ⅰ)由題設圖像知,周期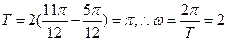 .
.
因為點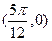 在函數圖像上,所以
在函數圖像上,所以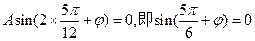 .
.
又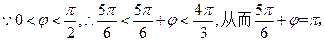 即
即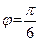 .
.
又點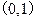 在函數圖像上,所以
在函數圖像上,所以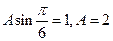 ,故函數f(x)的解析式為
,故函數f(x)的解析式為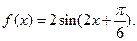
(Ⅱ)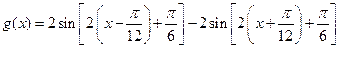
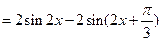
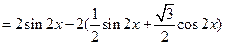
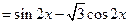
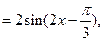
由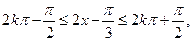 得
得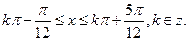
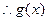 的單調遞增區間是
的單調遞增區間是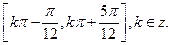
【點評】本題主要考查三角函數的圖像和性質.第一問結合圖形求得周期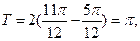 從而求得
從而求得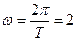 .再利用特殊點在圖像上求出
.再利用特殊點在圖像上求出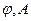 ,從而求出f(x)的解析式;第二問運用第一問結論和三角恒等變換及
,從而求出f(x)的解析式;第二問運用第一問結論和三角恒等變換及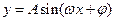 的單調性求得.
的單調性求得.