20.(本題滿分14分)本題共有2個小題,第1小題滿分6分,第2小題滿分8分
已知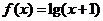 .
.
(1)若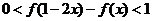 ,求
,求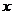 的取值范圍;
的取值范圍;
(2)若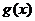 是以2為周期的偶函數,且當
是以2為周期的偶函數,且當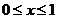 時,
時,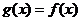 ,求函數
,求函數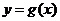 (
(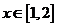 )的反函數.
)的反函數.
【答案與解析】

【點評】本題主要考查函數的概念、性質等基礎知識以及數形結合思想,熟練掌握指數函數、對數函數、冪函數的圖象與性質是關鍵,屬于中檔題.
21.(本題滿分14分)本題共有2個小題,第1小題滿分6分,第2小題滿分8分
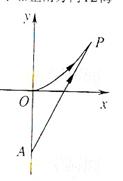
海事救援船對一艘失事船進行定位:以失事船的當前位置為原點,以正北方向為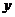 軸正方向建立平面直角坐標系(以1海里為單位長度),則救援船恰好在失事船正南方向12海里
軸正方向建立平面直角坐標系(以1海里為單位長度),則救援船恰好在失事船正南方向12海里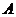 處,如圖,現假設:①失事船的移動路徑可視為拋物線
處,如圖,現假設:①失事船的移動路徑可視為拋物線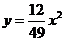 ;②定位后救援船即刻沿直線勻速前往救援;③救援船出發
;②定位后救援船即刻沿直線勻速前往救援;③救援船出發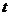 小時后,失事船所在位置的橫坐標為
小時后,失事船所在位置的橫坐標為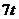 .
.
(1)當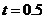 時,寫出失事船所在位置
時,寫出失事船所在位置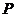 的縱坐標,若此時兩船恰好會合,求救援船速度的大小和方向;
的縱坐標,若此時兩船恰好會合,求救援船速度的大小和方向;
(2)問救援船的時速至少是多少海里才能追上失事船?
【答案與解析】


【點評】本題主要考查函數的概念、性質及導數等基礎知識.選擇恰當的函數模型是解決此類問題的關鍵,屬于中檔題.考查靈活運算數形結合、分類討論的思想方法進行探究、分析與解決問題的能力.屬于中檔偏上題目,也是近幾年高考的熱點問題.
22.(本題滿分16分)本題共有3個小題,第1小題滿分5分,第2小題滿分5分,第3小題滿分6分
在平面直角坐標系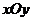 中,已知雙曲線
中,已知雙曲線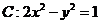 .
.
(1)設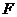 是
是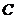 的左焦點,
的左焦點,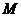 是
是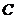 右支上一點,若
右支上一點,若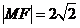 ,求點
,求點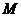 的坐標;
的坐標;
(2)過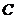 的左焦點作
的左焦點作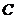 的兩條漸近線的平行線,求這兩組平行線圍成的平行四邊形的面積;
的兩條漸近線的平行線,求這兩組平行線圍成的平行四邊形的面積;
(3)設斜率為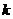 (
(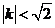 )的直線
)的直線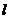 交
交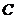 于
于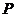 、
、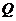 兩點,若
兩點,若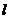 與圓
與圓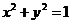 相切,求證:
相切,求證: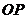 ⊥
⊥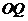 .
.
【答案與解析】


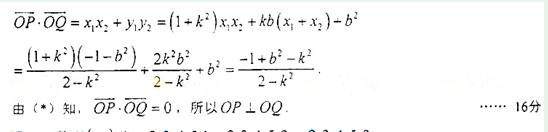
【點評】本題主要考查雙曲線的概念、標準方程、幾何性質及其直線與雙曲線的關系.特別要注意直線與雙曲線的關系問題,在雙曲線當中,最特殊的為等軸雙曲線,它的離心率為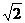 ,它的漸近線為
,它的漸近線為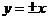 ,并且相互垂直,這些性質的運用可以大大節省解題時間,本題屬于中檔題 .
,并且相互垂直,這些性質的運用可以大大節省解題時間,本題屬于中檔題 .
23.(本題滿分18分)本題共有3個小題,第1小題滿分4分,第2小題滿分6分,第3小題滿分8分
對于項數為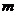 的有窮數列
的有窮數列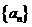 ,記
,記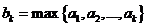 (
(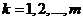 ),即
),即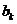 為
為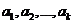 中的最大值,并稱數列
中的最大值,并稱數列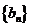 是
是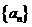 的控制數列,如1,3,2,5,5的控制數列是1,3,3,5,5.
的控制數列,如1,3,2,5,5的控制數列是1,3,3,5,5.
(1)若各項均為正整數的數列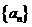 的控制數列為2,3,4,5,5,寫出所有的
的控制數列為2,3,4,5,5,寫出所有的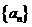 ;
;
(2)設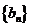 是
是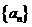 的控制數列,滿足
的控制數列,滿足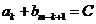 (
(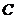 為常數,
為常數,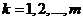 ),求證:
),求證: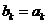 (
(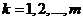 );
);
(3)設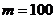 ,常數
,常數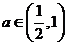 ,若
,若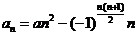 ,
,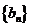 是
是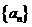 的控制數列,求
的控制數列,求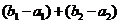
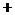
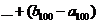 .
.
【答案與解析】

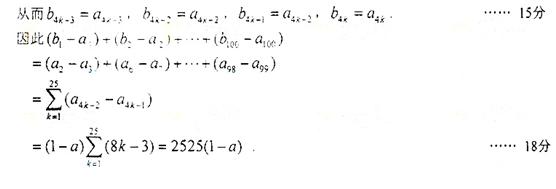
【點評】本題主要考查數列的通項公式、等差、等比數列的基本性質等基礎知識,本題屬于信息給予題,通過定義“控制”數列,考查考生分析探究及推理論證的能力.綜合考查數列的基本運算,數列問題一直是近幾年的命題重點內容,應引起足夠的重視.











