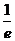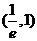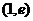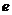三、解答題 :本大題共6小題,共74分.解答應寫出文字說明,證明過程或驗算步驟.
:本大題共6小題,共74分.解答應寫出文字說明,證明過程或驗算步驟.

(II)由(I)可知
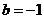 ,故方程(
,故方程( )即為
)即為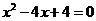 ,解得
,解得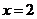 ,將其代入
,將其代入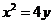 ,
, 得y=1,故點A(2,1).
得y=1,故點A(2,1).
因為圓A與拋物線C的準線相切 ,所以圓心A到拋物線C的準線y=-1的距離等于圓A的半徑r,
,所以圓心A到拋物線C的準線y=-1的距離等于圓A的半徑r,
即r=|1-(-1)|=2,所以圓A的方程為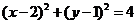 .
.
【命題立意】本題主要考查直線、圓、拋物線等基礎知識,考查運算求解能力,考查函數與方程思想、數形結合思想.

又基本事件的總數為10,故所求的概率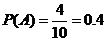 .
.
【命題立意】本題主要考查概率、統計等基礎知識,考查數據處理能力、運算求解能力、應用意識,考查函數與方程思想、分類與整體思想、必然與或然思想.
20.(本小題滿分12分)
如圖,四棱錐P-ABCD中,PA⊥底面ABCD,AB⊥AD,點E在線段AD上,且CE∥AB。
(1) 求證:CE⊥平面PAD;
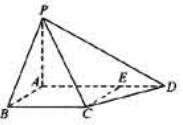 (11)若PA=AB=1,AD=3,CD=
(11)若PA=AB=1,AD=3,CD=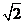 ,∠CDA=45°,求四棱錐P-ABCD的體積
,∠CDA=45°,求四棱錐P-ABCD的體積
【解析】(1)證明:因為PA⊥平面ABCD,CE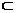 平面ABCD,所以PA⊥CE,
平面ABCD,所以PA⊥CE,
因為AB⊥AD,CE∥AB,所以CE⊥AD,又PA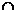 AD=A,所以CE⊥平面PAD.
AD=A,所以CE⊥平面PAD.
(2)解:由(1)可知CE⊥AD,在直角三角形ECD中,DE=CD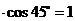 ,CE=CD
,CE=CD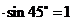 .
.

(2)作出平面區域(即三角形區域ABC)如圖,其中A(1,0),B(1,1),C(0,1),則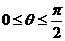 ,
,
又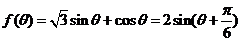 ,且
,且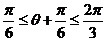 ,
,
故當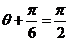 ,即
,即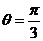 時,
時,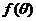 取得最大值2;當
取得最大值2;當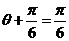 ,即
,即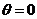 時,
時,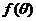 取得最小值1.
取得最小值1.
【命題立意】本題主要考查三角函數、不等式等基礎知識,考查運算求解能力、推理論證能力,考查函數與方程思想、數形結合思想、化歸與轉化思想.

由(2)可得,當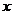 在區間
在區間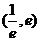 內變化時,
內變化時, 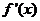 ,
,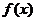 的變化情況如下表:
的變化情況如下表:
|
|
| 1 |
|
|
| - | 0 | + | ||
|
| 單調遞減 | 極小值1 | 單調遞增 | 2 |
又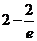 <2,所以函數
<2,所以函數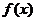

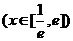 的值域為[1,2].
的值域為[1,2].

【命題立意】本題主要考查函數、導數等基礎知識,考查推理論證能力、抽象概括能力、運算求解能力,考查函數與方程思想、數形結合思想、化歸與轉化思想、分類與整合思想.