2013年普通高等學校招生全國統一考試
數學(文)(北京卷)參考答案
一、選擇題(共8小題,每小題5分,共40分)
1.B 2.D 3.C 4.A 5.B 6.C 7.C 8.B
二、填空題(共6小題,每小題5分,共30分)
9.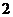 ,
,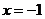 10.
10.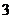 11.
11.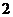 ,
,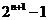
12.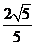 13.
13.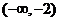 14.
14.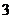
三、解答題(共6小題,共80分。解答應寫出必要的文字說明,演算步驟)
15.(本小題共13分)
解:(1)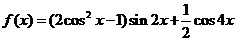
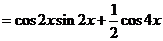
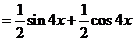
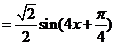
所以,最小正周期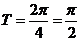
當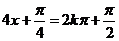 (
(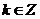 ),即
),即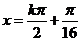 (
(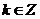 )時
)時
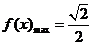
(2)因為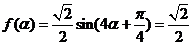
所以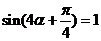
因為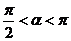 ,所以
,所以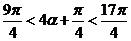
所以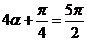 ,即
,即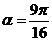
16.(本小題共13分)
解:(1)因為要停留2天,所以應該在3月1日至13日中的某天到達,共有13種選擇,其間重度污染的有兩天,
所以概率為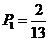
(2)此人停留的兩天共有13種選擇,分別是: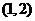 ,
,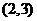 ,
,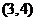 ,
,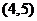 ,
,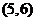 ,
,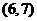 ,
,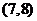 ,
,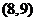 ,
,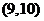 ,
,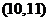 ,
,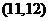 ,
,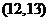 ,
,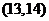
其中只有一天重度污染的為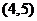 ,
,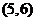 ,
,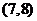 ,
,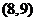 ,共4種,
,共4種,
所以概率為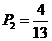
(3)因為第5,6,7三天的空氣質量指數波動最大,所以方差最大。
17.(本小題共14分)
證明:(1)因為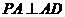 ,平面
,平面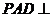 底面
底面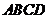 且平面
且平面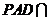 底面
底面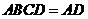
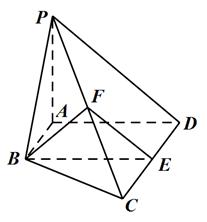
所以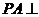 底面
底面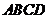
(2)因為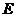 和
和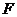 分別是
分別是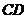 和
和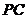 的中點,所以
的中點,所以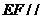
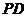 ,
,
而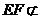 平面
平面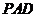 ,
,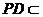 平面
平面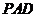 ,所以
,所以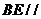 平面
平面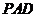
(3)因為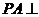 底面
底面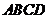 ,
, 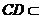 平面
平面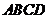
所以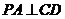 ,即
,即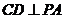
因為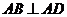 ,
,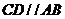 ,所以
,所以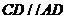
而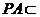 平面
平面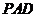 ,
,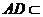 平面
平面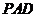 ,且
,且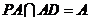
所以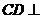 平面
平面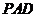
因為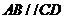 ,所以
,所以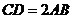 ,所以四邊形
,所以四邊形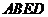 是平行四邊形,
是平行四邊形,
所以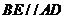 ,而
,而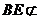 平面
平面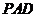 ,
,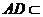 平面
平面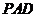
所以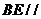 平面
平面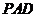 ,同理
,同理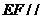 平面
平面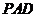 ,
,
而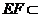 平面
平面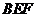 ,
,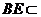 平面
平面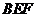 且
且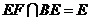
所以平面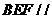 平面
平面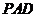 , 所以
, 所以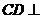 平面
平面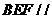
又因為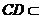 平面
平面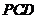
所以平面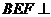 平面
平面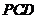
18.(本小題共13分)
解:(1)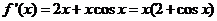
因為曲線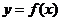 在點
在點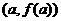 處的切線為
處的切線為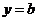
所以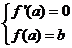 ,即
,即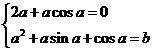 ,解得
,解得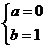
(2)因為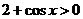
所以當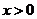 時
時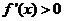 ,
,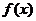 單調遞增
單調遞增
當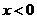 時
時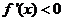 ,
,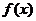 單調遞減
單調遞減
所以當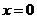 時,
時,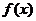 取得最小值
取得最小值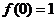 ,
,
所以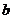 的取值范圍是
的取值范圍是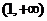
19.(本小題共14分)
解:(1)線段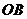 的垂直平分線為
的垂直平分線為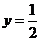 ,
,
因為四邊形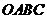 為菱形,
為菱形,
所以直線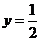 與橢圓的交點即為
與橢圓的交點即為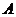 ,
,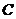 兩點
兩點
對橢圓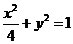 ,令
,令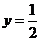 得
得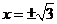
所以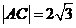
(2)方法一:當點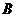 不是
不是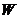 的頂點時,
的頂點時,
聯立方程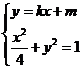 得
得
設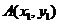 ,
,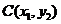 ,
,
則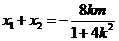 ,
,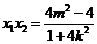 ,
,
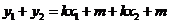
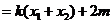
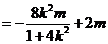
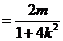
若四邊形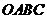 為菱形,則
為菱形,則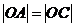 ,即
,即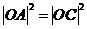
所以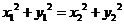
即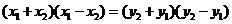
因為點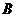 不是
不是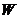 的頂點,所以
的頂點,所以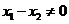 ,
,
所以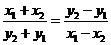
即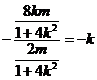 ,即
,即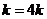
所以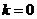
此時,直線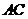 與
與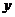 軸垂直,所以
軸垂直,所以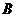 為橢圓的上頂點或下頂點,與已知矛盾,
為橢圓的上頂點或下頂點,與已知矛盾,
所以四邊形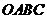 不可能為菱形
不可能為菱形
方法二:
因為四邊形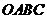 為菱形,所以
為菱形,所以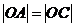 ,
,
設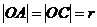 (
(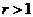 )
)
則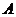 ,
,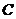 兩點為圓
兩點為圓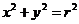 與橢圓
與橢圓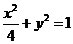 的交點
的交點
聯立方程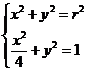 得
得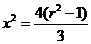
所以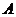 ,
,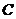 兩點的橫坐標相等或互為相反數。
兩點的橫坐標相等或互為相反數。
因為點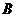 在
在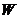 上
上
若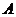 ,
,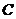 兩點的橫坐標相等,點
兩點的橫坐標相等,點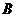 應為橢圓的左頂點或右頂點。不合題意。
應為橢圓的左頂點或右頂點。不合題意。
若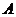 ,
,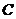 兩點的橫坐標互為相反數,點
兩點的橫坐標互為相反數,點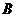 應為橢圓的上頂點或下頂點。不合題意。
應為橢圓的上頂點或下頂點。不合題意。
所以四邊形 不可能為菱形。
不可能為菱形。
20.(本小題共13分)
解:(1)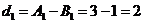 ,
,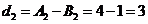 ,
,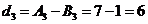
(2)因為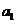 ,
,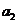 ,
,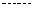 ,
,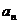 (
(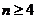 )是公比大于
)是公比大于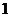 的等比數列,且
的等比數列,且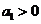
所以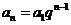
所以當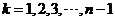 時,
時,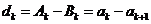
所以當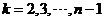 時,
時,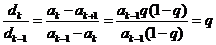
所以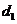 ,
,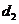 ,
,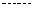 ,
,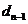 是等比數列。
是等比數列。
(3)若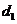 ,
,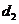 ,
,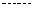 ,
,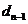 是公差大于
是公差大于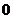 的等差數列,則
的等差數列,則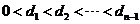
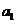 ,
,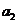 ,
,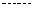 ,
,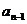 應是遞增數列,證明如下:
應是遞增數列,證明如下:
設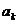 是第一個使得
是第一個使得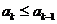 的項,則
的項,則
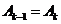 ,
,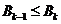 ,所以
,所以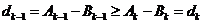 ,與已知矛盾。
,與已知矛盾。
所以,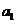 ,
,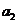 ,
,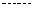 ,
,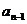 是遞增數列
是遞增數列
再證明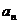 數列
數列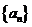 中最小項,否則
中最小項,否則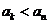 (
(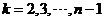 ),則
),則
顯然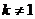 ,否則
,否則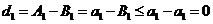 ,與
,與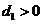 矛盾
矛盾
因而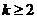 ,此時考慮
,此時考慮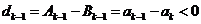 ,矛盾
,矛盾
因此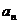 是數列
是數列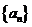 中最小項
中最小項
綜上,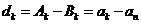 (
(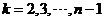 )
)
于是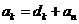 ,也即
,也即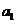 ,
,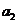 ,
,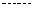 ,
,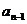 是等差數列
是等差數列











