一、本大題共8小題,每小題5分,共40分。在每小題列出的四個(gè)選項(xiàng)中,選出符合題目要求的一項(xiàng)。
1.在復(fù)平面內(nèi),復(fù)數(shù)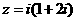 對(duì)應(yīng)的點(diǎn)位于
對(duì)應(yīng)的點(diǎn)位于
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.已知向量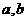 不共線,
不共線,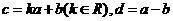 如果
如果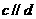 ,那么
,那么
A.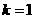 且
且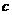 與
與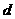 同向B.
同向B.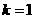 且
且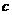 與
與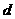 反向
反向
C.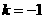 且
且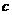 與
與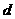 同向D.
同向D.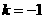 且
且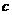 與
與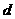 反向
反向
3.為了得到函數(shù)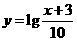 的圖像,只需把函數(shù)
的圖像,只需把函數(shù)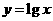 的圖像上所有的點(diǎn)
的圖像上所有的點(diǎn)
A.向左平移3個(gè)單位長度,再向上平移1個(gè)單位長度
B.向右平移3個(gè)單位長度,再向上平移1個(gè)單位長度
C.向左平移3個(gè)單位長度,再向下平移1個(gè)單位長度
D.向右平移3個(gè)單位長度,再向下平移1個(gè)單位長度
4.若正四棱柱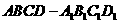 的底面邊長為1,
的底面邊長為1,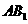 與底面
與底面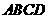 成60°角,則
成60°角,則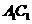 到底面
到底面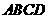 的距離為
的距離為
A.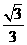 B.1 C.
B.1 C.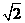 D.
D.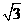
5.“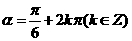 ”是“
”是“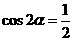 ”的
”的
A.充分而不必要條件 B.必要而不充分條件
C.充分必要條件 D.既不充分也不必要條件
6.若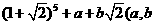 為有理數(shù)),則
為有理數(shù)),則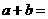
A.45 B.55 C.70D.80
7.用0到9這10個(gè)數(shù)字,可以組成沒有重復(fù)數(shù)字的三位偶數(shù)的個(gè)數(shù)為
A.324 B.328 C.360D.648
8.點(diǎn)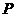 在直線
在直線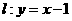 上,若存在過
上,若存在過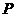 的直線交拋物線
的直線交拋物線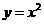 于
于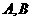 兩點(diǎn),且
兩點(diǎn),且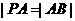 ,則稱點(diǎn)
,則稱點(diǎn)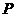 為“點(diǎn)”,那么下列結(jié)論中正確的是
為“點(diǎn)”,那么下列結(jié)論中正確的是
A.直線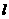 上的所有點(diǎn)都是“
上的所有點(diǎn)都是“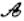 點(diǎn)”
點(diǎn)”
B.直線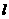 上僅有有限個(gè)點(diǎn)是“
上僅有有限個(gè)點(diǎn)是“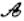 點(diǎn)”
點(diǎn)”
C.直線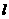 上的所有點(diǎn)都不是“
上的所有點(diǎn)都不是“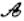 點(diǎn)”
點(diǎn)”
D.直線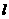 上有無窮多個(gè)點(diǎn)(點(diǎn)不是所有的點(diǎn))是“
上有無窮多個(gè)點(diǎn)(點(diǎn)不是所有的點(diǎn))是“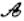 點(diǎn)”
點(diǎn)”
第Ⅱ卷(共110分)
二、填空題:本大題共6小題,每小題5分,共30分。把答案填在題中橫線上。
9.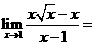 ___________。
___________。
10.若實(shí)數(shù)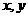 滿足
滿足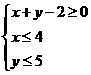 則
則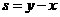 的最小值為__________。
的最小值為__________。
11.設(shè)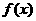 是偶函數(shù),若曲線
是偶函數(shù),若曲線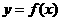 在點(diǎn)
在點(diǎn)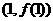 處的切線的斜率為1,則該曲線在點(diǎn)
處的切線的斜率為1,則該曲線在點(diǎn)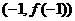 處的切線的斜率為______________。
處的切線的斜率為______________。
12.橢圓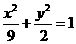 的焦點(diǎn)為
的焦點(diǎn)為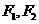 ,點(diǎn)
,點(diǎn)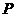 在橢圓上,若
在橢圓上,若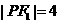 ,則
,則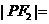 _________;
_________;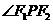 的小大為____________。
的小大為____________。
13.若函數(shù)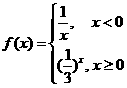 則不等式
則不等式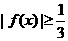 的解集為____________。
的解集為____________。
14.已知數(shù)列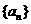 滿足:
滿足: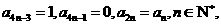 則
則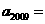 ________;
________;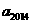 =____________。
=____________。
三 、解答題:本大題共6小題,共80分。解答應(yīng)寫出文字說明,演算步驟或證明過程。
15.(本小題共13分)
在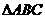 中,角
中,角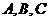 的對(duì)邊分別為
的對(duì)邊分別為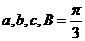 ,
,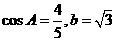 。
。
(I)求 的值;
的值;
(Ⅱ)求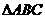 的面積。
的面積。
16.(本小題共14分)
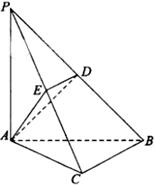
如圖,在三棱錐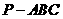 中,
中,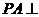 底面
底面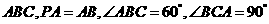 ,點(diǎn)
,點(diǎn)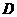 ,
,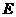 分別在棱
分別在棱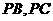 上,且
上,且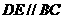
(I)求證: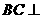 平面
平面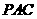 ;
;
(Ⅱ)當(dāng)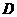 為
為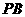 的中點(diǎn)時(shí),求
的中點(diǎn)時(shí),求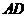 與平面
與平面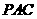 所成的角的大小;
所成的角的大小;
(Ⅲ)是否存在點(diǎn)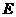 使得二面角
使得二面角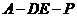 為直二面角?并說明理由。
為直二面角?并說明理由。
17.(本小題共13分)
某學(xué)生在上學(xué)路上要經(jīng)過4個(gè)路口,假設(shè)在各路口是否遇到紅燈是相互獨(dú)立的,遇到紅燈的概率都是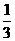 ,遇到紅燈時(shí)停留的時(shí)間都是2min。
,遇到紅燈時(shí)停留的時(shí)間都是2min。
(Ⅰ)求這名學(xué)生在上學(xué)路上到第三個(gè)路口時(shí)首次遇到紅燈的概率; 

(Ⅱ)求這名學(xué)生在上學(xué)路上因遇到紅燈停留的總時(shí)間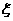 的分布列及期望。
的分布列及期望。
18.(本小題共13分)
設(shè)函數(shù)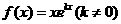
(I)求曲線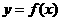 在點(diǎn)
在點(diǎn)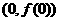 處的切線方程;
處的切線方程;
(Ⅱ)求函數(shù)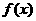 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅲ)若函數(shù)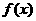 在區(qū)間
在區(qū)間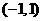 內(nèi)單調(diào)遞增,求
內(nèi)單調(diào)遞增,求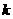 的取值范圍。
的取值范圍。
19.(本小題共14分)
已知雙曲線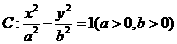 的離心率為
的離心率為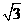 ,右準(zhǔn)線方程為
,右準(zhǔn)線方程為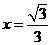
(I)求雙曲線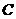 的方程;
的方程;
(Ⅱ)設(shè)直線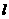 是圓
是圓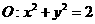 上動(dòng)點(diǎn)
上動(dòng)點(diǎn)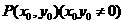 處的切線,
處的切線,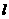 與雙曲線
與雙曲線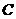 交于不同的兩點(diǎn)
交于不同的兩點(diǎn)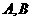 ,證明
,證明 的大小為定值。
的大小為定值。
20.(本小題共13分)
已知數(shù)集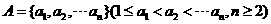 具有性質(zhì)
具有性質(zhì)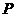 ;對(duì)任意的
;對(duì)任意的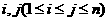 ,
,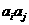 與
與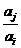 兩數(shù)中至少有一個(gè)屬于
兩數(shù)中至少有一個(gè)屬于 。
。
(I)分別判斷數(shù)集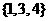 與
與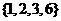 是否具有性質(zhì)
是否具有性質(zhì)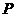 ,并說明理由;
,并說明理由;
(Ⅱ)證明: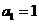 ,且
,且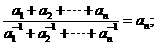
(Ⅲ)證明:當(dāng)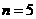 時(shí),
時(shí),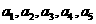 成等比數(shù)列。
成等比數(shù)列。











