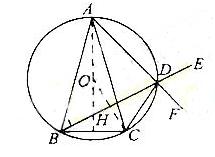
(20)(本小題滿分12分)
已知,橢圓C過點(diǎn)A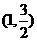 ,兩個焦點(diǎn)為(-1,0),(1,0)。
,兩個焦點(diǎn)為(-1,0),(1,0)。
(1) 求橢圓C的方程; 
(2) E,F是橢圓C上的兩個動點(diǎn),如果直線AE的斜率與AF的斜率互為相反數(shù),證明直線EF的斜率為定值,并求出這個定值。
(20)解:
(Ⅰ)由題意,c=1,可設(shè)橢圓方程為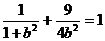 ,解得
,解得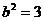 ,
,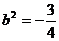 (舍去)
(舍去)
所以橢圓方程為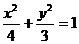 。 ……………4分
。 ……………4分
(Ⅱ)設(shè)直線AE方程為: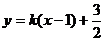 ,代入
,代入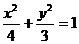 得
得
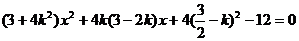
設(shè)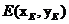 ,
,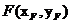 ,因?yàn)辄c(diǎn)
,因?yàn)辄c(diǎn)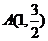 在橢圓上,所以
在橢圓上,所以
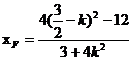
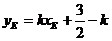 ………8分
………8分
又直線AF的斜率與AE的斜率互為相反數(shù),在上式中以—K代K,可得
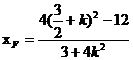
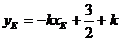
所以直線EF的斜率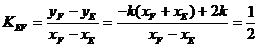
即直線EF的斜率為定值,其值為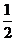 。 ……12分
。 ……12分
(21)(本小題滿分12分)
已知函數(shù)f(x)=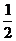 x
x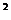 -ax+(a-1)
-ax+(a-1)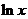 ,
,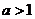 。
。
(1)討論函數(shù)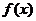 的單調(diào)性;
的單調(diào)性;
(2)證明:若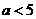 ,則對任意x
,則對任意x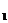 ,x
,x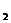
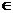
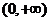 ,x
,x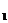
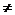 x
x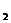 ,有
,有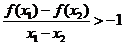 。
。
(21)解:(1)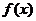 的定義域?yàn)?img onmouseover='upNext(this)' title="1411377126209054.gif" src="http://pic.kekenet.com/2014/0922/1411377281616416.gif" border="0"/>。
的定義域?yàn)?img onmouseover='upNext(this)' title="1411377126209054.gif" src="http://pic.kekenet.com/2014/0922/1411377281616416.gif" border="0"/>。
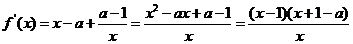 2分
2分
(i)若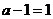 即
即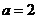 ,則
,則
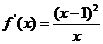
故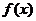 在
在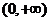 單調(diào)增加。
單調(diào)增加。
(ii)若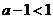 ,而
,而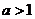 ,故
,故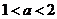 ,則當(dāng)
,則當(dāng)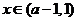 時,
時,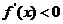 ;
;
當(dāng)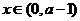 及
及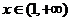 時,
時,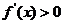
故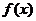 在
在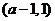 單調(diào)減少,在
單調(diào)減少,在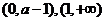 單調(diào)增加。
單調(diào)增加。
(iii)若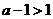 ,即
,即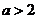 ,同理可得
,同理可得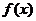 在
在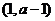 單調(diào)減少,在
單調(diào)減少,在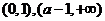 單調(diào)增加.
單調(diào)增加.
(II)考慮函數(shù) 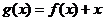
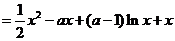
則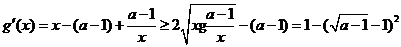
由于1<a<5,故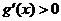 ,即g(x)在(4, +∞)單調(diào)增加,從而當(dāng)
,即g(x)在(4, +∞)單調(diào)增加,從而當(dāng)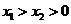 時有
時有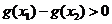 ,即
,即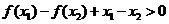 ,故
,故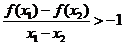 ,當(dāng)
,當(dāng)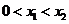 時,有
時,有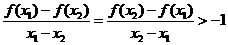 ·········12分
·········12分
請考生在第(22)、(23)、(24)三題中任選一題做答,如果多做,則按所做的第一題記分。做答時用2B鉛筆在答題卡上把所選題目的題號涂黑。
(22)(本小題滿分10分)選修4-1:幾何證明講
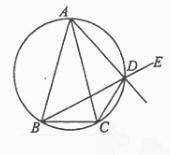
已知 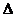 ABC 中,AB=AC, D是
ABC 中,AB=AC, D是 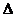 ABC外接圓劣弧
ABC外接圓劣弧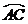 上的點(diǎn)(不與點(diǎn)A,C重合),延長BD至E。
上的點(diǎn)(不與點(diǎn)A,C重合),延長BD至E。
(1) 求證:AD的延長線平分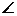 CDE;
CDE;
(2) 若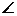 BAC=30,
BAC=30,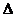 ABC中BC邊上的高為2+
ABC中BC邊上的高為2+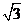 ,求
,求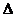 ABC外接圓的面積。
ABC外接圓的面積。

(22)解:
(Ⅰ)如圖,設(shè)F為AD延長線上一點(diǎn)
∴∠CDF=∠ABC
又AB=AC ∴∠ABC=∠ACB,
且∠ADB=∠ACB, ∴∠ADB=∠CDF,
對頂角∠EDF=∠ADB, 故∠EDF=∠CDF,
即AD的延長線平分∠CDE.
(Ⅱ)設(shè)O為外接圓圓心,連接AO交BC于H,則AH⊥BC.
連接OC,A由題意∠OAC=∠OCA=150, ∠ACB=750,
∴∠OCH=600.
設(shè)圓半徑為r,則r+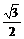 r=2+
r=2+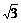 ,a得r=2,外接圓的面積為4
,a得r=2,外接圓的面積為4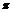 。
。
(23)(本小題滿分10分)選修4-4 :坐標(biāo)系與參數(shù)方程在直角坐標(biāo)系xOy中,以O(shè)為極點(diǎn),x正半軸為極軸建立極坐標(biāo)系,曲線C的極坐標(biāo)方程為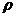 cos(
cos(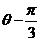 )=1,M,N分別為C與x軸,y軸的交點(diǎn)。
)=1,M,N分別為C與x軸,y軸的交點(diǎn)。
(1)寫出C的直角坐標(biāo)方程,并求M,N的極坐標(biāo); 
(2)設(shè)MN的中點(diǎn)為P,求直線OP的極坐標(biāo)方程。
(23)解:
(Ⅰ)由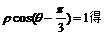
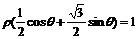
從而C的直角坐標(biāo)方程為
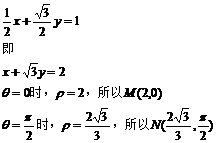
(Ⅱ)M點(diǎn)的直角坐標(biāo)為(2,0)
N點(diǎn)的直角坐標(biāo)為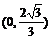
所以P點(diǎn)的直角坐標(biāo)為
所以直線OP的極坐標(biāo)方程為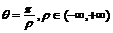
(24)(本小題滿分10分)選修4-5:不等式選講
設(shè)函數(shù)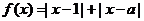 。
。
(1) 若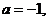 解不等式
解不等式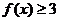 ;
;
(2)如果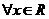 ,
,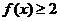 ,求
,求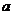 的取值范圍。
的取值范圍。
(24)解:
(Ⅰ)當(dāng)a=-1時,f(x)=︱x-1︳+︱x+1︳.
由f(x)≥3得
︱x-1︳+︱x+1|≥3
(ⅰ)x≤-1時,不等式化為
1-x-1-x≥3 即-2x≥3