(18)(本小題滿分13分。(Ⅰ)小題6分(Ⅱ)小題7分。)
設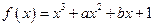 的導數
的導數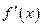 滿足
滿足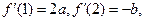 其中常數
其中常數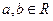 .
.
(Ⅰ)求曲線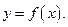 在點
在點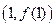 處的切線方程。
處的切線方程。
(Ⅱ)設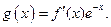 求函數
求函數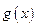 的極值。
的極值。
解析:(Ⅰ)因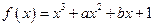 ,故
,故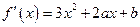 ,
,
令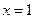 ,得
,得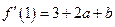 ,由已知
,由已知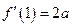 ,解得
,解得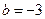
(19)本小題滿分12分,(Ⅰ)小問5分,(Ⅱ)小問7分。
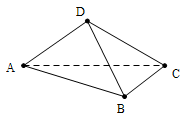
如圖, 在四面體
在四面體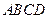 中,平面
中,平面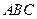 ⊥
⊥ 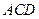 ,
, 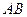 ⊥
⊥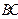 ,
,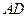 =
=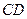 ,∠
,∠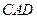 =
=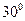
(Ⅰ)若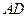 =2,
=2,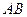 =2
=2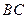 ,求四邊形
,求四邊形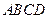 的體積。
的體積。
(Ⅱ)若二面角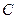 -
-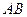 -
-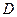 為
為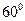 ,求異面直線
,求異面直線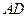 與
與 所成角的余弦值。
所成角的余弦值。
解析:(Ⅰ)如圖所示,設F為AC的中點,由于AD=CD,所以DF⊥AC.
故由平面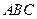 ⊥
⊥ 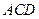 ,知DF⊥平面
,知DF⊥平面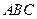 ,即
,即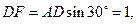 ,
,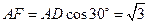 。在
。在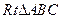 中,因
中,因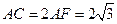 ,AB=2BC,有勾股定理易得
,AB=2BC,有勾股定理易得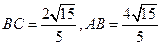 .
.
故四面體ABCD的體積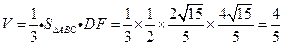
(Ⅱ)如圖所示設G、H分別為變CD,BD的中點,則FG//AD,GH//BC,,從而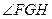 是異面直線
是異面直線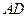 與
與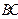 所成角或其補角。
所成角或其補角。

設E為邊AB的中點,則EF//BC,由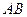 ⊥
⊥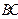 ,知
,知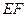 ⊥
⊥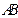 ,又由(Ⅰ)有DF⊥平面
,又由(Ⅰ)有DF⊥平面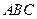 ,故由三垂線定理知
,故由三垂線定理知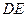 ⊥
⊥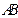 ,所以
,所以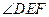 為二面角
為二面角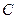 -
-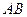 -
-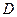 的平面角,由題設知
的平面角,由題設知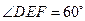 ,設AD=a,則DF=ADsinCAD=
,設AD=a,則DF=ADsinCAD=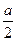
解析:(Ⅰ)由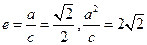 ,解得
,解得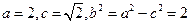 ,
,
故橢圓的標準方程為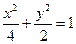
(Ⅱ)設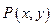 ,
,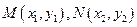 ,則由
,則由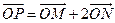 得
得
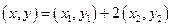 ,即
,即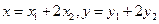 ,
,

(21)(本小題滿 分12分。(Ⅰ)小問5分,(Ⅱ)小問7分)
分12分。(Ⅰ)小問5分,(Ⅱ)小問7分)
設實數數列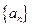 的前n項和
的前n項和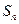 滿足
滿足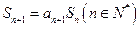
(Ⅰ)若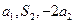 成等比數列,求
成等比數列,求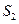 和
和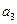
(Ⅱ)求證:對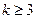 有
有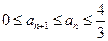 。
。
解析:(Ⅰ)由題意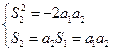 ,得
,得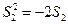 ,
,
由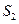 是等比中項知
是等比中項知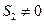 ,因此
,因此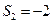 ,
,
由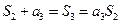 ,解得,
,解得,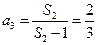
(Ⅱ)證明:有題設條件有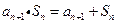 ,
,
故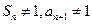 ,且
,且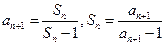
從而對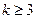 有
有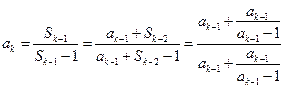 ①
①












