一、選擇題:本大題共10小題,每小題5分,共50分。在每小題給出的四個備選項中,只有一項是符合題目要求的。

3.曲線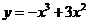 在點(1,2)處的切線方程為
在點(1,2)處的切線方程為
(A) 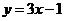 (B)
(B) 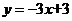 (C)
(C)
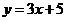 (D)
(D)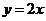
【命題意圖】本題考查利用導數求函數的切線,是容易題.
【解析】∵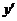 =
=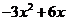 ,∴切線斜率為3,則過(1,2)的切線方程為
,∴切線斜率為3,則過(1,2)的切線方程為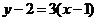 ,即
,即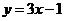 ,故選A.
,故選A.
【答案】A
4.從一堆蘋果中任取10只稱得它的質量如下(單位:克)
125 120 122 105 130 114 116 95 120 134
則樣本數據落在[114.5,124.5) 內的頻率為
內的頻率為
(A)0.2 (B)0.3 (C)0.4 (D)0.5

6.設 =
=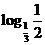 ,
,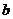 =
=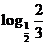 ,
, =
=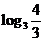 ,則
,則 ,
,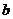 ,
, 的大小關系是
的大小關系是
(A)  <
<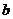 <
< (B)
(B) 
 <
<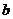 <
< (C)
(C) 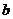 <
< <
< (D)
(D) 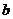 <
< <
<
【命題意圖】本題考查對數函數的圖像與性質,是簡單題.
【解析】∵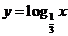 與
與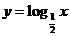 在(0,+∞)都是減函數,且0<
在(0,+∞)都是減函數,且0<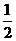 <1,0<
<1,0<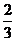 <1,
<1,
∴ =
=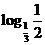 >0,
>0,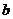 =
=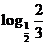 >0,
>0,
又∵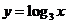 在(0,+∞)上是增函數,且0<
在(0,+∞)上是增函數,且0<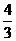 <1,∴
<1,∴ =
=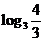 <0,即
<0,即 最小,只有B符合,故選B.
最小,只有B符合,故選B.
【答案】B
7.若函數 =
=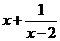 (
( >2)在
>2)在 =
= 處有最小值,則
處有最小值,則 =
=
(A)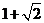 (B)
(B)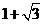
 (C)3 (D)4
(C)3 (D)4

9.設雙曲線的左準線與兩條漸近線交于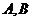 兩點,左焦點為在以
兩點,左焦點為在以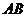 才為之直徑的圓內,則該雙曲線的離心率的取值范圍為
才為之直徑的圓內,則該雙曲線的離心率的取值范圍為
(A)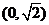 (B)
(B)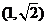 (C)
(C) 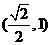 (D)
(D)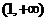
【命題意圖】本題考查雙曲線的性質、點與圓的位置關系,考查學生轉化與化歸能力、解不等式能力,難度較大.
【解析】雙曲線的左準線為 =
=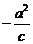 ,漸近線方程為
,漸近線方程為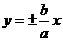 ,聯立解得(
,聯立解得(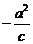 ,
,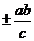 ),
),
∴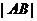 =
=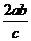 ,根據題意得,
,根據題意得,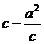 <
<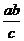 ,即
,即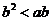 ,即
,即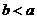 ,即
,即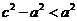 ,即
,即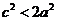 ,即
,即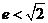 ,又
,又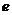 >1,,1<
>1,,1<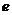 <
<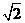 ,故選B.
,故選B.
【答案】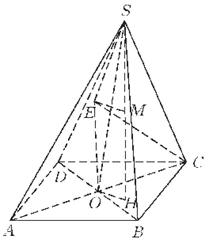 B
B
10.高為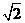 的四棱錐
的四棱錐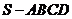 的底面是邊長為
的底面是邊長為 1的正方形,點
1的正方形,點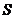 、
、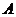 、
、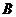 、
、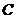 、
、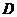 均在半徑為1的同一球面上,則底面
均在半徑為1的同一球面上,則底面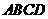 的中心與頂點
的中心與頂點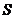 之間的距離為
之間的距離為
(A)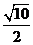 (B)
(B)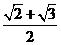 (C)
(C)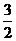 (D)
(D)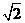
【命題意圖】本題考查四棱錐與其外接球的相關知識,考查空間想象能力、轉化化歸能力以及運算求解能力,是難題.
【解析】如圖,設四棱錐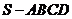 的外接球球心為
的外接球球心為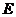 ,則
,則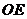 ⊥面
⊥面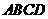 ,在
,在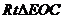 中,
中,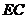 =1,
=1,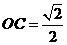 ,∴
,∴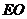 =
=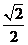 ,
,
∵設四棱錐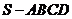 的高
的高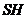 =
=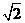 ,∴
,∴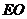 ∥
∥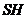 且
且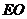 =
=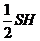 ,
,
取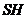 的中點
的中點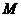 ,連結
,連結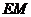 ,則四邊形
,則四邊形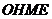 為矩形,∴
為矩形,∴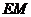 ⊥
⊥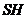 ,
,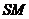 =
=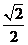 ,在
,在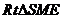 中,
中,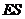 =1,則
=1,則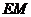 =
=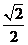 ,∴
,∴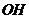 =
=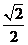 ,
,
 在
在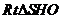 中,
中,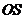 =
=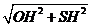 =
=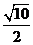 ,故選A.
,故選A.
【答案】A











