二.填空題,本大題共5小題,每小題5分,共25分,把答案填寫在答題卡相應位置上
11. 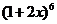 的展開式中
的展開式中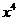 的系數是___________.
的系數是___________.

14.從甲、乙等10位同學中任選3位去參加某項活動,則所選3位中有甲但沒有乙的概率為_________
【命題意圖】本題考查組合計算和等可能事件的概率計算,是中檔題.
【解析】10位同學任選3人共有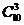 種選法,其中含甲不含乙共有
種選法,其中含甲不含乙共有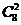 種選法,故所選3位中有甲但沒有乙的概率為
種選法,故所選3位中有甲但沒有乙的概率為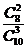 =
=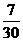 .
.
【答案】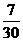
15.若實數 ,
,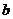 ,
, 滿足
滿足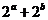 =
=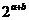 ,
,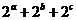 =
=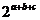 ,則
,則 的最大值是 .
的最大值是 .
【命題意圖】本題考查基本不等式的應用,指數、對數等相關知識,考查了轉化與化歸思想,是難題.
【解析】∵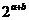 =
=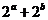 ≥
≥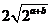 ,∴
,∴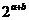 ≥4,
≥4,
又∵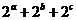 =
=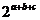 ,∴
,∴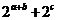 =
=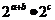 ,∴
,∴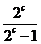 =
=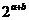 ≥4,即
≥4,即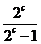 ≥4,即
≥4,即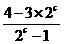 ≥0,∴
≥0,∴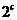 ≤
≤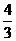 ,∴
,∴ ≤
≤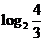 =
=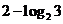 ,∴
,∴ 的最大值為
的最大值為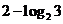 .
.
【答案】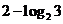

三、解答是:本大題共6小題,共75分 .解
.解 答應寫出文字說明、證明過程或演算步驟.
答應寫出文字說明、證明過程或演算步驟.
16.(本小題滿分 13分,(Ⅰ)小問7分,(Ⅱ)小問6分.)設{
13分,(Ⅰ)小問7分,(Ⅱ)小問6分.)設{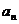 }是公比為正數的等比數列,
}是公比為正數的等比數列,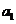 =2,
=2,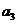 =
=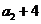 .
.
(Ⅰ)求{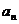 }的通項公式;
}的通項公式;
(Ⅱ)設{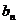 }是首項為1,公差為2的等差數列,求數列{
}是首項為1,公差為2的等差數列,求數列{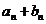 }的前
}的前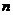 項和
項和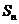 .
.
【命題意圖】本題考查等比數列的通項公式和等比數列、等差數列的前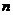 項和公式,考查函數與方程思想和運算求解能力,是簡單題.
項和公式,考查函數與方程思想和運算求解能力,是簡單題.
【解析】(Ⅰ)設等比數列{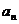 }的公比為
}的公比為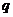 ,由
,由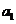 =2,
=2,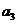 =
=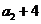 知,
知,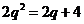 ,
,
即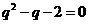 ,解得
,解得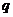 =2或
=2或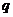 =-1(舍去),∴
=-1(舍去),∴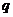 =2,
=2,
∴{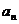 }的通項公式
}的通項公式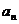 =
=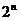 (
(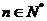 );
);
(Ⅱ) 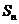 =
=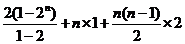 =
=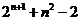 .
.
17.(本小題滿分13分,(Ⅰ)小問6分,(Ⅱ)小問7分.)某市公租房的房源位于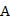 、
、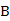 、
、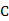 三個片區.設每位申請人只申請其中一個片區的房源,且申請其中任一個片區的房源是等可能的.求該市的4位申請人中:
三個片區.設每位申請人只申請其中一個片區的房源,且申請其中任一個片區的房源是等可能的.求該市的4位申請人中:
(Ⅰ)沒有人申請A片區房源的概率;
(Ⅱ)每個片區的房源都有人申 請的概
請的概 率.
率.
【命題意圖】本題考查應用排列組合知識和兩個計數原理求等可能事件的概率、獨立重復試驗,考查運用概率知識分析解決問題能力,是中檔題.
【解析】(Ⅰ) (法1)設事件A表示 “沒有人申請A片區房源”所有可能的申請方式有
“沒有人申請A片區房源”所有可能的申請方式有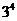 種,其中沒有人申請A片區房源方式有
種,其中沒有人申請A片區房源方式有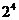 種,則沒有人申請A片區房源的概率為
種,則沒有人申請A片區房源的概率為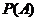 =
=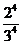 =
=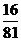 .
.
(法2)設“申請A片區房源”為事件A,
∵每位申請人只申請其中一個片區的房源,且申請其中任一個片區的房源是等可能的,
∴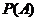 =
=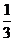 ,
,
對每位申請房源作為一次試驗,應為每人申請房源相 互獨立,4人申請房源可以看成4次獨立重復試驗,故沒人申請A片房源的概率為
互獨立,4人申請房源可以看成4次獨立重復試驗,故沒人申請A片房源的概率為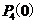 =
=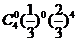 =
=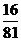 ;
;
(Ⅱ)記“每個片區的房源都有人申請”為事件B,所有可能的申請方式有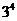 種,其中每個片區的房源都有人申請的方式有
種,其中每個片區的房源都有人申請的方式有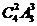 種,
種,
∴每個片區的房源都有人申請的概率為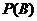 =
=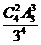 =
=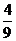 .
.
18. (本小題滿分13分,(Ⅰ)小問7分,(Ⅱ)小問6分.)設函數 =
=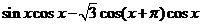 (
(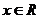 ).
).
(Ⅰ)求 的最小正周期;
的最小正周期;
(Ⅱ)若函數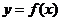 的圖象按
的圖象按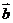 =(
=(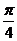 ,
,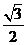 )平移后得到函數
)平移后得到函數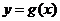 的圖象,求
的圖象,求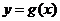 在[0,
在[0,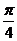 ]上的
]上的 最大值.
最大值.
【命題意圖】本題考查誘導公式、兩 角和與差的正余弦公式、周期公式、向量平移、三角函數在某個區間上的最值求法和運算求解能力,是中檔題.
角和與差的正余弦公式、周期公式、向量平移、三角函數在某個區間上的最值求法和運算求解能力,是中檔題.
【解析】(Ⅰ)  =
=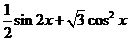 =
=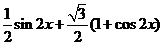
=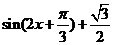 ,
,
∴ 的最小正周期為
的最小正周期為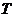 =
=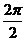 =
=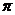 .
.
(Ⅱ)依題意得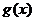 =
=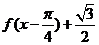 =
=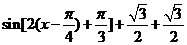
=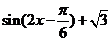
當 ∈[0,
∈[0,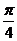 ]時,
]時,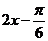 ∈
∈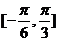 ,∴
,∴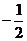 ≤
≤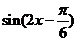 ≤
≤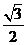 ,
,
∴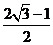 ≤
≤ ≤
≤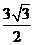 , ∴
, ∴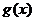 在[0,
在[0,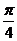 ]的最大值為
]的最大值為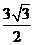 .
.











