19. (本小題滿分12分,(Ⅰ)小問5分,(Ⅱ )小問7分.)
)小問7分.)
設 =
=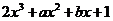 的導數為
的導數為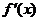 ,若函數
,若函數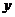 =
=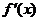 的圖象關于直線
的圖象關于直線 =
=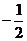 對稱,且
對稱,且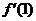 =0.
=0.
(Ⅰ)求實數 ,
,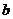 的值;
的值;
(Ⅱ)求函數 的極值.
的極值.
【命題意圖】本題考查考查利用導數求函數的極值、二次函數的圖像與性質,考查方程與不等式思想、轉化和化歸思想,屬容易題.
【解析】(Ⅰ)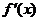 =
=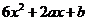 ,
,
∵若函數
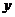 =
=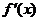 的圖象關于直線
的圖象關于直線 =
=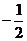 對稱,且
對稱,且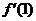 =0,
=0,
∴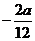 =
=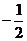 且
且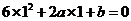 ,解得
,解得 =3,
=3,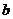 =-12.
=-12.
(Ⅱ)由(Ⅰ)知 =
=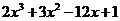 ,
,
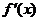 =
=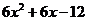 =
=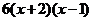 ,
,
 的變化如下:
的變化如下:
| (-∞,-2) | -2 | (-2,1) | 1 | (1,+∞) |
| + | 0 | - | 0 | + |
|
| 極大值21 |
| 極小值-6 |
|
∴當 =-2時,
=-2時, 取極大值,極大值為21,當
取極大值,極大值為21,當 =1時,
=1時, 取極小值,極小值為-6.
取極小值,極小值為-6.
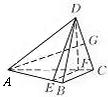
20.(本小題滿分12分,(Ⅰ)小問6分,(Ⅱ )小問6分.如圖,在四面體
)小問6分.如圖,在四面體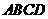 中,平面
中,平面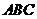 ⊥平面
⊥平面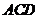 ,
,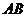 ⊥
⊥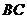 ,
,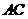 =
=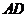 =2,
=2,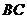 =
=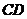 =1.
=1.

(Ⅰ)求四面體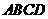 的體積;
的體積;
(Ⅱ)求二面角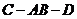 的平面角的正切值.
的平面角的正切值.
【命題意圖】本題考查簡單幾何體的體積計算、二面角的求法,考查空間想象能力、推理論證能力、運算求解能力及轉化與化歸思想,是中檔題.
【解析】(Ⅰ) 如圖,過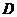 作
作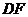 ⊥
⊥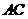 于
于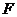 ,∵平面
,∵平面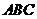 ⊥平面
⊥平面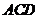 ,
,
∴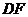 ⊥平面
⊥平面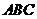 ,則
,則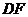 是四面體
是四面體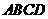 的面
的面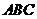 上的高,
上的高,
設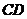 中點為
中點為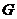 ,∵
,∵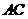 =
=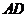 =2,∴
=2,∴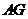 ⊥
⊥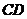 ,
,
∴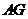 =
=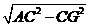 =
=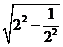 =
=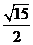 ,
,
∵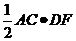 =
=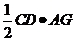 , ∴
, ∴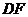 =
=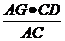 =
=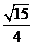 ,
,
在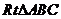 中,
中,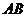 =
=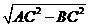 =
=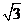 ,∴
,∴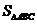 =
=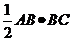 =
=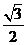 ,
,
∴四棱錐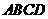 的體積
的體積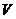 =
=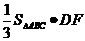 =
=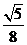 .
.
(Ⅱ)(幾何法)過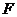 作
作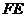 ⊥
⊥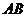 與
與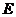 ,連結
,連結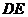 ,由(Ⅰ)知
,由(Ⅰ)知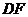 ⊥面
⊥面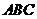 ,
,
由三垂線定理知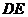 ⊥
⊥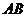 ,∴
,∴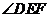 為二面角
為二面角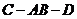 的平面角,
的平面角,
在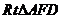 中,
中,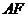 =
=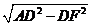 =
=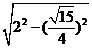 =
=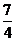 ,
,
在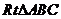 中,
中,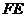 ∥
∥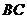 , ∴
, ∴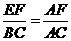 , ∴
, ∴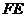 =
=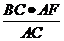 =
=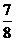 ,
,
在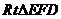 中,
中,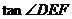 =
=
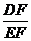 =
=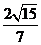 .
.

21. ( 本小題滿分12分,(Ⅰ)小問4分,(Ⅱ)小問8分.)如圖,橢圓的中心為原點
本小題滿分12分,(Ⅰ)小問4分,(Ⅱ)小問8分.)如圖,橢圓的中心為原點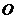 ,離心率
,離心率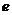 =
=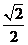 ,一條準線的方程是
,一條準線的方程是 =
=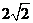 .
.
(Ⅰ)求橢圓的標準方程;
(Ⅱ)設動點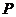 滿足:
滿足: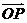 =
=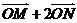 ,其中
,其中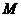 ,
,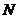 是橢圓上的點,直線
是橢圓上的點,直線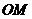 與
與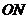 的斜率之積為
的斜率之積為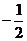 .問:是否存在定點
.問:是否存在定點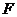 ,使得
,使得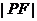 與點
與點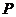 到直線
到直線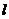 :
: =
=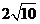 的距離之比為定值?若存在,求
的距離之比為定值?若存在,求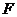 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.
【命題意圖】本題考查了橢圓標準方程的求解與橢圓的定植問題,考查學生綜合運用知識解決問題能力、運算求解能力和探究問題能力,難度較大.
【解析】(Ⅰ) ∵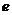 =
=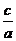 =
=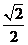 ,
,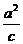 =
=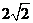 ,解得
,解得 =2,
=2,
 =
=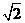 ,∴
,∴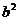 =
=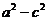 =2,
=2,
∴橢圓的標準方程為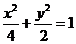 ;
;
(Ⅱ)設P( ,
,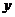 ),
),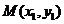 ,
,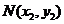 ,
, 則由
則由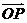 =
=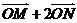 ,得
,得
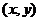 =
=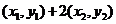 =
=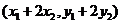 ,
,
∴ =
=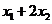 ,
,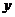 =
=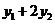 ,
,
∵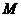 ,
,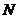 在橢圓
在橢圓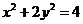 上,∴
上,∴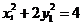 ,
,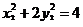 ,
,
∴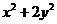 =
=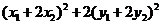 =
=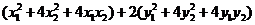
=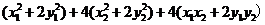 =
=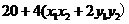 .
.
設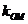 ,
,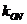 分別表示直線
分別表示直線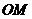 ,
,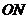 的斜率,由題設條件知,
的斜率,由題設條件知,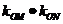 =
=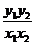 =
=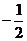 ,
,
∴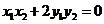 , ∴
, ∴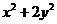 =20,
=20,
∴點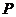 在橢圓
在橢圓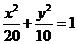 上,該橢圓的右焦點為
上,該橢圓的右焦點為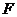 (
(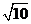 ,0),離心率
,0),離心率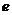 =
=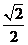 ,右準線為
,右準線為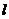 :
: =
=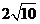 ,
,
∴根據橢圓的第二定義,存在定點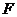 (
(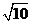 ,0),使得
,0),使得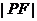 與點
與點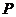 到直線
到直線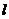 的距離之比為定值.
的距離之比為定值.