一.填空題:本大題共10小題,每小題5分,共計50分。在每小題給出的四個備選選項中,只有一個是符合題目要求的
1.在等差數(shù)列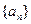 中,
中,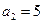 則
則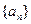 的前5項和
的前5項和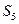 =
=
A.7 B.15C.20 D.25
2.不等式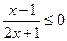 的解集為
的解集為
A.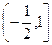 B.
B.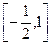 C.
C.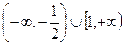 D.
D.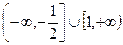
【答案】 A
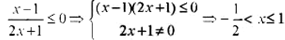
【解析】
【考點定位】本題主要考察了分式不等式的解法,解題的關(guān)鍵是靈活運用不等式的性質(zhì),屬于基礎(chǔ)試題
3.對任意的實數(shù)k,直線y=kx+1與圓 的位置關(guān)系一定是
A. 相離 B.相切 C.相交但直線不過圓心D.相交且直線過圓心
相離 B.相切 C.相交但直線不過圓心D.相交且直線過圓心
【答案】C
4.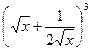 的展開式中常數(shù)項為
的展開式中常數(shù)項為
A.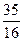 B.
B.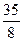 C.
C.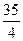 D.105
D.105
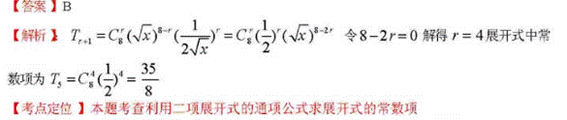
(5)設(shè)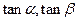 是議程
是議程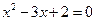 的兩個根,則
的兩個根,則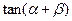 的值為
的值為
(A)-3 (B)-1(C)1 (D)3

(6)設(shè)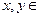 R,向量
R,向量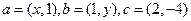 且
且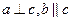 ,則
,則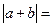
(A)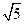 (B)
(B)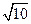 (C)
(C)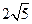 (D)10
(D)10

(7)已知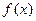 是定義在R上的偶函數(shù),且以2為周期,則“
是定義在R上的偶函數(shù),且以2為周期,則“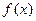 為[0,1]上的增函數(shù)”是“
為[0,1]上的增函數(shù)”是“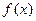 為[3,4]上的減函數(shù)”的
為[3,4]上的減函數(shù)”的
(A)既不充分也不必要的條件 (B)充分而不必要的條件
(C)必要而不充分的條件(D)充要條件
【答案】D
【解析】由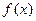 是定義在R上的偶函數(shù)及[0,1]雙抗的增函數(shù)可知在[-1,0]減函數(shù),又2為周期,所以【3,4】上的減函數(shù)
是定義在R上的偶函數(shù)及[0,1]雙抗的增函數(shù)可知在[-1,0]減函數(shù),又2為周期,所以【3,4】上的減函數(shù)
【考點定位】本題主要通過常用邏輯用語來考察函數(shù)的奇偶性,進(jìn)而來考察函數(shù)的周期性,根據(jù)圖像分析出函數(shù)的性質(zhì)及其經(jīng)過的特殊點是解答本題的關(guān)鍵。
(8)設(shè)函數(shù)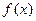 在R上可導(dǎo),其導(dǎo)函數(shù)為
在R上可導(dǎo),其導(dǎo)函數(shù)為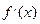 ,且函數(shù)
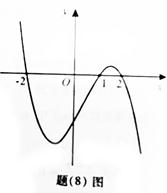
,且函數(shù)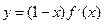 的圖像如題(8)圖所示,則下列結(jié)論中一定成立的是
的圖像如題(8)圖所示,則下列結(jié)論中一定成立的是
(A)函數(shù)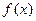 有極大值
有極大值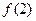 和極小值
和極小值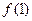
(B)函數(shù)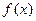 有極大值
有極大值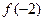 和極小值
和極小值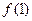
(C)函數(shù)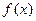 有極大值
有極大值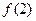 和極小值
和極小值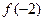
(D)函數(shù)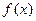 有極大值
有極大值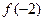 和極小值
和極小值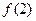

(9)設(shè)四面體的六條棱的長分別為1,1,1,1,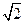 和
和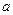 ,且長為
,且長為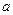 的棱與長為
的棱與長為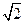 的棱異面,則
的棱異面,則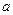 的取值范圍是
的取值范圍是
(A)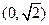 (B)
(B)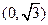 (C)
(C)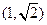 (D)
(D)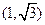

(10)設(shè)平面點集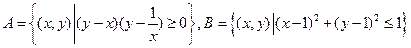 ,則
,則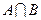 所表示的平面圖形的面積為
所表示的平面圖形的面積為
(A)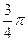 (B)
(B)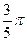 (C)
(C)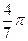 (D)
(D)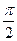

二 填空題:本大題共5小題,每小題5分,共25分,把答案分別填寫在答題卡相應(yīng)位置上
(11)若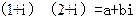 ,其中
,其中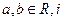 為虛數(shù)單位,則
為虛數(shù)單位,則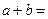 ;
;
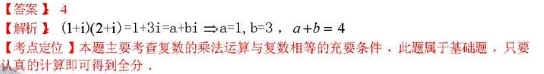
(12)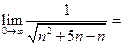 。
。
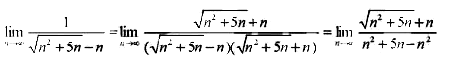
【答案】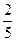
【解析】
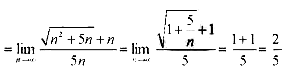
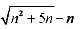
【考點定位】本題考查極限的求法和應(yīng)用,因都沒有極限,可先分母有理化再求極限
(13)設(shè)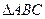 的內(nèi)角
的內(nèi)角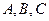 的對邊分別為
的對邊分別為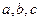 ,且
,且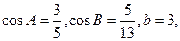 則
則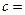

(14)過拋物線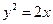 的焦點
的焦點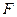 作直線交拋物線于
作直線交拋物線于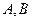 兩點,若
兩點,若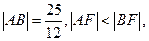 則
則
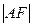 =。
=。

(15)某藝校在一天的6節(jié)課中隨機安排語文、數(shù)學(xué)、外語三門文化課和其他三門藝術(shù)課個1節(jié),則在課表上的相鄰兩節(jié)文化課之間最多間隔1節(jié)藝術(shù)課的概率為 (用數(shù)字作答).
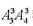 【答案】
【答案】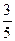
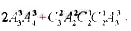
【解析】語文、數(shù)學(xué)、英語三門文化課間隔一節(jié)藝術(shù)課,排列有種排法,語文、數(shù)學(xué)、英語三門文化課相鄰有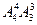 種排法,語文、數(shù)學(xué)、英語三門文化課兩門相鄰有
種排法,語文、數(shù)學(xué)、英語三門文化課兩門相鄰有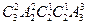 種排法。故所有的排法種數(shù)有在課表上的相鄰兩節(jié)文化課之間最多
種排法。故所有的排法種數(shù)有在課表上的相鄰兩節(jié)文化課之間最多
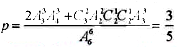
間隔1節(jié)藝術(shù)課的概率為
【考點定位】本題在計數(shù)時根據(jù)具體情況運用了插空法,做題時要注意體會這些方法的原理及其實際意義。











