第二部分(非選擇題 共110分)
二、填空題共6小題,每小題5分,共30分。
(9)在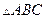 中,若
中,若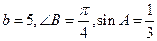 ,則
,則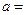
 .
.
【答案】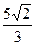
【解析】:由正弦定理得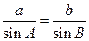 又
又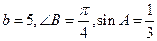 所以
所以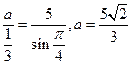
(10)已知雙曲線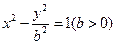 的一條漸近線的方程為
的一條漸近線的方程為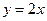 ,則
,則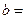 .
.
【答案】2
【解析】:由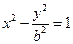 得漸近線的方程為
得漸近線的方程為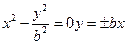 即
即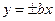 ,由一條漸近線的方程為
,由一條漸近線的方程為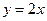 得
得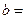 2
2
(11)已知向量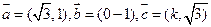 。若
。若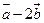 與
與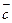 ,共線,則
,共線,則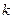 =.
=.
 【答案】1
【答案】1
【解析】: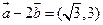 由
由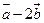 與
與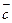 共線得
共線得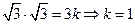
(12)在等比數(shù)列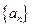 中,若
中,若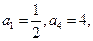 則公比
則公比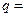
 ;
;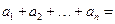
【答案】2 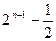
【解析】:由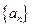 是等比數(shù)列得
是等比數(shù)列得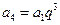 ,又
,又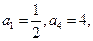 所以
所以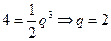
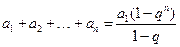
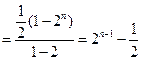
(13)已知函 數(shù)
數(shù)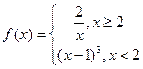 ,若關(guān)于
,若關(guān)于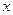 的方程
的方程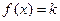 有兩個不同的實(shí)根,則實(shí)數(shù)
有兩個不同的實(shí)根,則實(shí)數(shù)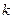 的取值范圍是.
的取值范圍是.
【答案】(0,1)
【解析】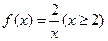 單調(diào)遞減且值域?yàn)?0,1],
單調(diào)遞減且值域?yàn)?0,1],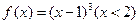 單調(diào)遞增且值域?yàn)?img onmouseover='upNext(this)' title="1416374485743582.gif" src="http://pic.kekenet.com/2014/1119/1416374719407640.gif" alt="2011年高考數(shù)學(xué)真題附解析(北京卷+文科)" />,
單調(diào)遞增且值域?yàn)?img onmouseover='upNext(this)' title="1416374485743582.gif" src="http://pic.kekenet.com/2014/1119/1416374719407640.gif" alt="2011年高考數(shù)學(xué)真題附解析(北京卷+文科)" />,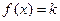 有兩個不同的實(shí)根,則實(shí)數(shù)k的取值范圍是(0,1)。
有兩個不同的實(shí)根,則實(shí)數(shù)k的取值范圍是(0,1)。
(14)設(shè)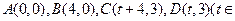 R)。記
R)。記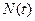 為平行四邊形ABCD內(nèi)部(不含邊界)的整點(diǎn)的個數(shù),其中整點(diǎn)是指橫、縱坐標(biāo)都是整數(shù)的點(diǎn),則
為平行四邊形ABCD內(nèi)部(不含邊界)的整點(diǎn)的個數(shù),其中整點(diǎn)是指橫、縱坐標(biāo)都是整數(shù)的點(diǎn),則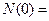 ;
;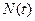 的所有可能取值為 。
的所有可能取值為 。
【答案】66,7,8,
【解析】:在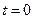 ,
,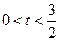 ,
,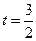 時分別對應(yīng)點(diǎn)為6,8 ,7。在平面直角坐標(biāo)系中畫出平行四邊形
時分別對應(yīng)點(diǎn)為6,8 ,7。在平面直角坐標(biāo)系中畫出平行四邊形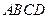 ,其中
,其中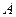 位于原點(diǎn),
位于原點(diǎn),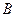 位于
位于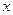 正半軸;設(shè)
正半軸;設(shè)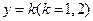 與
與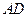 邊的交點(diǎn)為
邊的交點(diǎn)為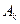 ,與
,與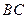 邊的交點(diǎn)為
邊的交點(diǎn)為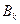 ,四邊形內(nèi)部
,四邊形內(nèi)部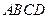 (不包括邊界)的整點(diǎn)都在線段
(不包括邊界)的整點(diǎn)都在線段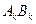 上,
上,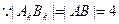
 線段
線段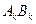 上的整點(diǎn)有3個或4個,所以
上的整點(diǎn)有3個或4個,所以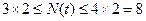 ,不難求得點(diǎn)
,不難求得點(diǎn)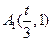 ,
,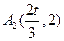
①當(dāng)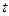 為
為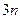 型整數(shù)時,都是整點(diǎn),
型整數(shù)時,都是整點(diǎn),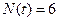
②當(dāng)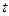 為
為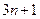 型整數(shù)時,
型整數(shù)時,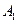 ,
,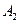 都不是整點(diǎn),
都不是整點(diǎn),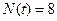
③當(dāng)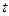 為
為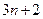 型整數(shù)時,
型整數(shù)時,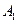 ,
,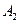 都不是整點(diǎn),
都不是整點(diǎn),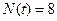 (以上表述中
(以上表述中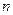 為整數(shù))
為整數(shù))
上面3種情形涵概了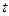 的所有整數(shù)取值,所以
的所有整數(shù)取值,所以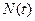 的值域?yàn)閧6,7,8 }
的值域?yàn)閧6,7,8 }











