評論
打印
三、解答題 （本大題共6小題，共74分.解答應寫出文字說明、證明過程或演算步驟.）
17．（12分）（2007•遼寧）某公司在過去幾年內使用某種型號的燈管1000支，該公司對這些燈管的使用壽命（單位：小時）進行了統計，統計結果如下表所示：
分組 [500，900） [900，1100） [1100，1300） [1300，1500） [1500，1700） [1700，1900） [1900，+∞）
頻數 48 121 208 223 193 165 42
頻率
（1）將各組的頻率填入表中；
（2）根據上述統計結果，計算燈管使用壽命不足1500小時的頻率；
（3）該公司某辦公室新安裝了這種型號的燈管2支，若將上述頻率作為概率，試求恰有1支燈管的使用壽命不足1500小時的概率．
【考點】 頻率分布表．
【專題】 計算題．
【分析】 （1）由頻率=
，可得出各組的頻率；
（2）要計算燈管使用壽命不足1500小時的頻率，即計算前四個小組的頻率之和；
（3）恰有1支燈管的使用壽命不足1500小時即1支燈管使用壽命不足1500小時，另一支燈管使用壽命超過1500小時，分為兩種情形，最后求出它們的和即可．
【解答】 解：（I）
分組 [500，900） [900，1100） [1100，1300） [1300，1500） [1500，1700） [1700，1900） [1900，+∞）
頻數 48 121 208 223 193 165 42
頻率 0.048 0.121 0.208 0.223 0.193 0.165 0.042
（4分）
（II）由（I）可得0.048+0.121+0.208+0.223=0.6，所以燈管使用壽命不足1500小時的頻率為0.6．（8分）
（III）由（II）知，1支燈管使用壽命不足1500小時的概率P1=0.6，另一支燈管使用壽命超過1500小時的概率P2=1﹣P1=1﹣0.6=0.4，則這兩支燈管中恰有1支燈管的使用壽命不足1500小時的概率是P1P2+P2P1=2×0.6×0.4=0.48．所以有2支燈管的使用壽命不足1500小時的概率是0.48．（12分）
【點評】 本題主要考查頻率分布表的計算和頻數分布直方圖的應用以及概率的求法，屬于基礎題．
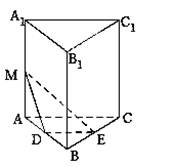
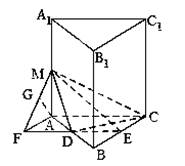
18．（12分）（2007•遼寧）如圖，在直三棱柱ABC﹣A1B1C1中，∠ACB=90°，AC=BC=a，D，E分別為棱AB，BC的中點，M為棱AA1上的點，二面角M﹣DE﹣A為30°．
（I）證明：A1B1⊥C1D；
（II）求MA的長，并求點C到平面MDE的距離．
【考點】 與二面角有關的立體幾何綜合題；棱柱的結構特征；點、線、面間的距離計算．
【專題】 計算題；證明題．
【分析】 （I）連接CD，根據三垂線定理可得AB⊥C1D，而A1B1平行AB，從而A1B1⊥C1D；
（II）過點A作CE的平行線，交ED的延長線于F，連接MF，根據定義可知∠MFA為二面角M﹣DE﹣A的平面角，在Rt△GAF中，∠GFA=30°，求出A到平面MDE的距離，再根據線面平行可知C到平面MDE的距離與A到平面MDE的距離相等．
【解答】 解：（I）證明：連接CD，
三棱柱ABC﹣A1B1C1是直三棱柱，∴CC1⊥平面ABC，∴CD為C1D在平面ABC內的射影．∵△ABC中，AC=BC，D為AB中點，∴AB⊥CD，∴AB⊥C1D∵A1B1∥AB，∴A1B1⊥C1D
（II）解：過點A作CE的平行線，
交ED的延長線于F，連接MF∵D，E分別為AB，BC的中點，∴DE∥AC
又∵AF∥CE，CE⊥AC∴AF⊥DE∵MA⊥平面ABC，∴AF為MF在平面ABC內的射影
∴MF⊥DE∴∠MFA為二面角M﹣DE﹣A的平面角，∠MFA=30°
在Rt△MAF中，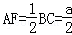
，∠MFA=30°，∴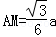
作AG⊥MF，垂足為G，∵MF⊥DE，AF⊥DE，∴DE⊥平面AMF，∵平面MDE⊥平面AMF，∴AG⊥平面MDE
在Rt△GAF中，∠GFA=30°，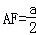
，∴
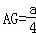，即A到平面MDE的距離為
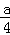∵CA∥DE，∴CA∥平面MDE，∴C到平面MDE的距離與A到平面MDE的距離相等，為．
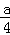【點評】 本小題主要考查空間中的線面關系，解三角形等基礎知識，考查空間想象能力與思維能力，屬于基礎題．
19．（12分）（2007•遼寧）已知函數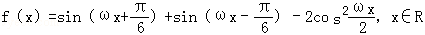
（其中ω＞0）
（I）求函數f（x）的值域；
（II）若函數y=f（x）的圖象與直線y=﹣1的兩個相鄰交點間的距離為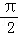
，求函數y=f（x）的單調增區間．
【考點】 由y=Asin（ωx+φ）的部分圖象確定其解析式；正弦函數的單調性．
【專題】 計算題．
【分析】 （I）利用兩角和與差的正弦函數、二倍角公式化簡不等式，然后利用兩角和化簡函數為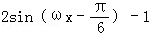
，解好正弦函數的有界性，求函數f（x）的值域；
（II）利用函數y=f（x）的圖象與直線y=﹣1的兩個相鄰交點間的距離為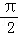，求出周期，求出ω，利用正弦函數的單調增區間，求函出數y=f（x）的單調增區間．
【解答】 解：（I）解：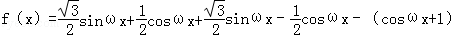
=
=．
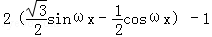
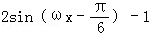【點評】 本小題主要考查三角函數公式，三角函數圖象和性質等基礎知識，考查綜合運用三角函數有關知識的能力，常考題．
20．（12分）（2007•遼寧）已知數列{an}，{bn}滿足a1=2，b1=1，且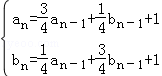
（n≥2）
（I）令cn=an+bn，求數列{cn}的通項公式；
（II）求數列{an}的通項公式及前n項和公式Sn．
【考點】 數列遞推式；等差數列的通項公式；數列的求和．
【專題】 計算題．
【分析】 （I）根據題意可求得cn=cn﹣1+2，進而根據等差數列的定義可推斷出{cn}是首項為a1+b1=3，公差為2的等差數列，進而求得其通項公式．
（II）令dn=an﹣bn，則可知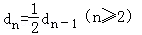
進而推斷出{dn}是首項為a1﹣b1=1，公比為
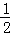的等比數列，則其通項公式可求，進而根據an﹣bn和an+bn的表達式，聯立方程求得an，進而根據等差數列和等比數列的求和公式求得答案．
【解答】 解：（I）由題設得an+bn=（an﹣1+bn﹣1）+2（n≥2），即cn=cn﹣1+2（n≥2）
易知{cn}是首項為a1+b1=3，公差為2的等差數列，通項公式為cn=2n+1
（II）解：由題設得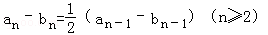
，令dn=an﹣bn，則
、
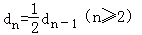易知{dn}是首項為a1﹣b1=1，公比為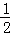
的等比數列，通項公式為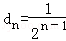
由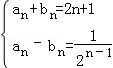
解得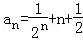
，
求和得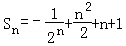
【點評】 本小題主要考查等差數列，等比數列等基礎知識，考查基本運算能力．
21．（14分）（2007•遼寧）已知正三角形OAB的三個頂點都在拋物線y2=2x上，其中O為坐標原點，設圓C是OAB的內接圓（點C為圓心）
（Ⅰ）求圓C的方程；
（Ⅱ）設圓M的方程為（x﹣4﹣7cosθ）2+（y﹣7cosθ）2=1，過圓M上任意一點P分別作圓C的兩條切線PE，PF，切點為E，F，求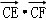
的最大值和最小值．
【考點】 圓的標準方程；平面向量數量積的運算；圓的切線方程．
【專題】 計算題；綜合題；壓軸題；函數思想．
【分析】 （Ⅰ）設出A、B的坐標（正三角形OAB的三個頂點都在拋物線y2=2x上），根據△ABO邊長相等，求出A、B點的坐標，再求圓心和半徑，進而求可得圓C的方程；
（Ⅱ）設出∠ECF=2α，表示出數量積，數量積中有cosα，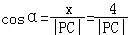
，確定|PC|的范圍，可求出數量積的最值．
【解答】 解：（Ⅰ）解法一：設A，B兩點坐標分別為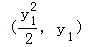
，
，
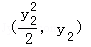由題設知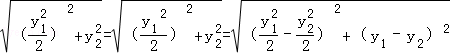
解得y12=y22=12，
所以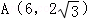
，
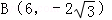或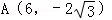
，
．
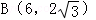設圓心C的坐標為（r，0），則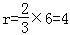
，
所以圓C的方程為（x﹣4）2+y2=16．
解法二：設A，B兩點坐標分別為（x1，y1），（x2，y2），由題設知x12+y12=x22+y22
又因為y12=2x1，y22=2x2，可得x12+2x1=x22+2x2．即（x1﹣x2）（x1+x2+2）=0
由x1＞0，x2＞0，可知x1=x2，故A，B兩點關于x軸對稱，所以圓心C在x軸上
設C點的坐標為（r，0），則A點坐標為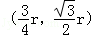
，于是有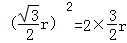
，
解得r=4，
所以圓C的方程為（x﹣4）2+y2=16．
（Ⅱ）解：設∠ECF=2α，則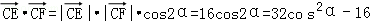
．
在Rt△PCE中，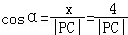
，由圓的幾何性質得|PC|≤|MC|+1=7+1=8，|PC|≥|MC|﹣1=7﹣1=6，
所以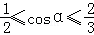
，由此可得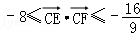
．
則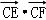
的最大值為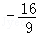
，最小值為﹣8．
【點評】 本小題主要考查平面向量，圓與拋物線的方程及幾何性質等基本知識，考查綜合運用解析幾何知識解決問題的能力．
22．（12分）（2007•遼寧）已知函數f（x）=x3﹣9x2cosα+48xcosβ+18sin2α，g（x）=f'（x），且對任意的實數t均有g（1+cost）≥0，g（3+sint）≤0．
（I）求函數f（x）的解析式；
（II）若對任意的m∈[﹣26，6]，恒有f（x）≥x2﹣mx﹣11，求x的取值范圍．
【考點】 函數解析式的求解及常用方法；函數恒成立問題．
【專題】 壓軸題．
【分析】 （1）先求出f'（x），即g（x），它是關于x的二次函數，對任意的實數t均有g（1+cost）≥0，g（3+sint）≤0
可先求出1+cost和3+sint的范圍，轉化為g（x）在某些區間上恒成立，結合二次函數的圖象確定g（x）應滿足的條件．
（2）由題意對任意的m∈[﹣26，6]恒成立，只要把式子看成關于m的不等式恒成立即可．
【解答】 解：（1）g（x）=f'（x）=3x2﹣18xcosα+48cosβ
對任意的實數t，1+cost∈[0，2]，3+sint∈[2，4]．
對任意的實數t有g（1+cost）≥0，g（3+sint）≤0
即對任意的實數x∈[0，2]有g（x）≥0，x∈[2，4]時有g（x）≤0
∴
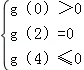即
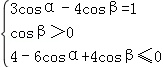，解得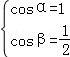
所以f（x）=x3﹣9x2+24x
（2）令g（m）=f（x）﹣x2+mx+11=xm+x3﹣10x2+24x+11
由題意只要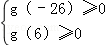
即
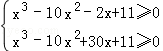，解得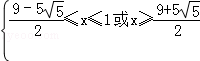
【點評】 本題考查待定系數法求解析式、不等式恒成立問題，綜合性強，難度較大．
