三、解答題：解答應寫出文字說明，證明過程或演算步驟。

（17）(本小題滿分12分)

在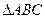中，角A，B，C的對邊分別為a，b，c。角A，B，C成等差數列。

(Ⅰ)求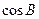的值；

(Ⅱ)邊a，b，c成等比數列，求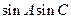的值。

（18）(本小題滿分12分)

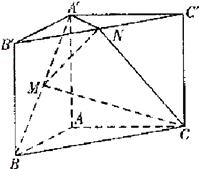
如圖，直三棱柱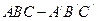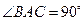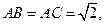，，AA′=1，點M，N分別為和的中點。

(Ⅰ)證明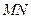：∥平面；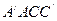

(Ⅱ)求三棱錐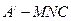的體積。（錐體體積公式V=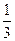Sh,其中S為底面面積，h為高）

（19）(本小題滿分12分)

電視傳媒公司為了了解某地區電視觀眾對某類體育節目的收視情況，隨機抽取了100名觀眾進行調查，其中女性有55名。下面是根據調查結果繪制的觀眾日均收看該體育節目時間的頻率分布直方圖；

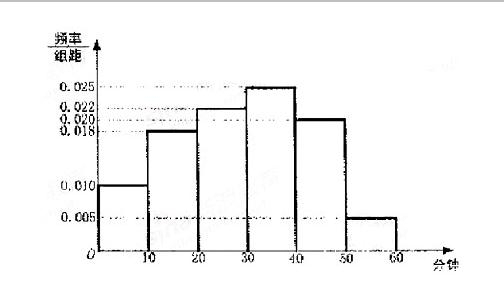
將日均收看該體育節目時間不低于40分鐘的觀眾稱為“體育迷”，已知“體育迷”中有10名女性。

(Ⅰ)根據已知條件完成下面的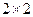列聯表，并據此資料你是否認為“體育迷”與性別有關？

(Ⅱ)將日均收看該體育項目不低于50分鐘的觀眾稱為“超級體育迷”，已知“超級體育迷”中有2名女性，若從“超級體育迷”中任意選取2人，求至少有1名女性觀眾的概率。

附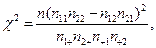

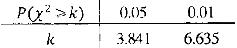
（20）(本小題滿分12分)

如圖，動圓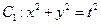,1<t<3,與橢圓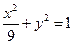：相交于A，B，C，D四點，點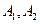分別為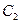的左，右頂點。

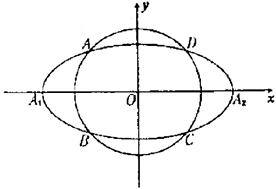
(Ⅰ)當t為何值時，矩形ABCD的面積取得最大值？并求出其最大面積；

(Ⅱ)求直線AA1與直線A2B交點M的軌跡方程。

（21）(本小題滿分12分)

設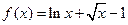，證明：

(Ⅰ)當x﹥1時， ﹤ （ ）；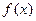

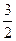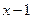(Ⅱ)當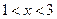時，。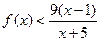

(22)(本小題滿分10分)選修41：幾何證明選講

如圖，⊙O和⊙相交于A，B兩點，過A作兩圓的切線分別交兩圓于C，D兩點，連接DB并延長交⊙O于點E。證明：

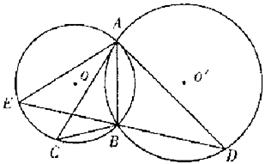
(Ⅰ)；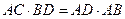

(Ⅱ) 。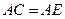

(23)(本小題滿分10分)選修44：坐標系與參數方程

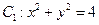在直角坐標中，圓，圓。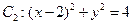

(Ⅰ)在以O為極點，x軸正半軸為極軸的極坐標系中，分別寫出圓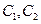的極坐標方程，并求出圓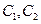的交點坐標(用極坐標表示)；

(Ⅱ)求圓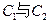的公共弦的參數方程。

(24)(本小題滿分10分)選修45：不等式選講

已知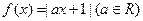，不等式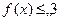的解集為{x|-2｝。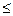

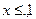(Ⅰ)求a的值；

(Ⅱ)若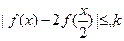恒成立，求k的取值范圍。

點擊此處下載文檔(rar格式，930.50KB)