18.(本小題滿分13分,(Ⅰ)小問(wèn)7分,(Ⅱ)小問(wèn)6分)
甲、乙兩人輪流投籃,每人每次投一球,約定甲先投且先投中者獲勝,一直每人都已投球3次時(shí)投籃結(jié)束,設(shè)甲每次投籃投中的概率為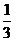 ,乙每次投籃投中的概率為
,乙每次投籃投中的概率為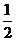 ,且各次投籃互不影響。(Ⅰ)求乙獲勝的概率;(Ⅱ)求投籃結(jié)束時(shí)乙只投了2個(gè)球的概率。
,且各次投籃互不影響。(Ⅰ)求乙獲勝的概率;(Ⅱ)求投籃結(jié)束時(shí)乙只投了2個(gè)球的概率。
【答案】:(Ⅰ)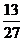 (Ⅱ)
(Ⅱ)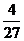
 獨(dú)立事件同時(shí)發(fā)生的概率計(jì)算公式知
獨(dú)立事件同時(shí)發(fā)生的概率計(jì)算公式知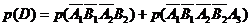
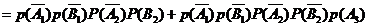
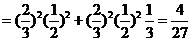
19.(本小題滿分12分,(Ⅰ)小問(wèn)5分,(Ⅱ)小問(wèn)7分)設(shè)函數(shù)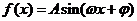 (其中
(其中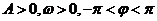 )在
)在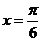 處取得最大值2,其圖象與軸的相鄰兩個(gè)交點(diǎn)的距離為
處取得最大值2,其圖象與軸的相鄰兩個(gè)交點(diǎn)的距離為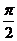 (I)求
(I)求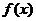 的解析式; (II)求函數(shù)
的解析式; (II)求函數(shù)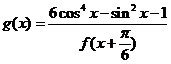 的值域。
的值域。
【答案】:(Ⅰ)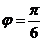 (Ⅱ)
(Ⅱ)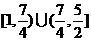

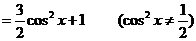 因
因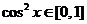 ,且
,且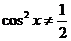
故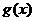 的值域?yàn)?img onmouseover='upNext(this)' title="1413518122673513.gif" src="http://pic.kekenet.com/2014/1017/1413518215205065.gif" alt="2012年高考數(shù)學(xué)真題附解析(重慶卷+文科)"/>
的值域?yàn)?img onmouseover='upNext(this)' title="1413518122673513.gif" src="http://pic.kekenet.com/2014/1017/1413518215205065.gif" alt="2012年高考數(shù)學(xué)真題附解析(重慶卷+文科)"/>
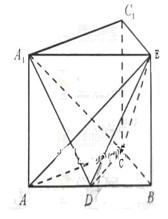
(20)(本小題滿分12分,(Ⅰ)小問(wèn)4分,(Ⅱ)小問(wèn)8分)已知直三棱柱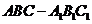 中,
中,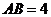 ,
,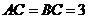 ,
,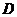 為
為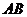 的中點(diǎn)。(Ⅰ)求異面直線
的中點(diǎn)。(Ⅰ)求異面直線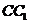 和
和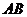 的距離;(Ⅱ)若
的距離;(Ⅱ)若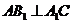 ,求二面角
,求二面角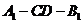 的平面角的余弦值。
的平面角的余弦值。
【答案】:(Ⅰ)(Ⅱ)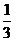
【解析】:(Ⅰ)如答(20)圖1,因AC=BC, D為AB的中點(diǎn),故CD 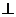 AB。又直三棱柱中,
AB。又直三棱柱中,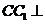 面
面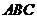 ,故
,故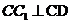 ,所以異面直線
,所以異面直線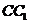 和AB的距離為
和AB的距離為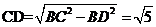
(Ⅱ):由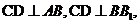 故
故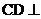 面
面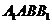 ,從而
,從而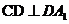 ,
,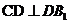 故
故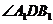 為所求的二面角
為所求的二面角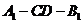 的平面角。
的平面角。
因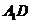 是
是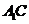 在面
在面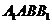 上的射影,又已知
上的射影,又已知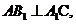 由三垂線定理的逆定理得
由三垂線定理的逆定理得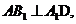 從而
從而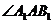 ,
,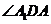 都與
都與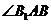 互余,因此
互余,因此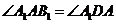 ,所以
,所以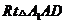 ≌
≌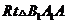 ,因此
,因此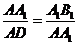 得
得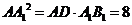
從而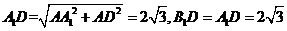
所以在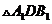 中,由余弦定理得
中,由余弦定理得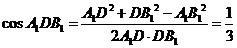
(21)(本小題滿分12分,(Ⅰ)小問(wèn)5分,(Ⅱ)小問(wèn)7分)
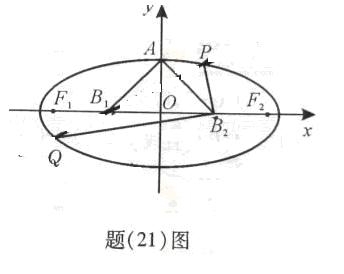
已知橢圓的中心為原點(diǎn)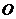 ,長(zhǎng)軸在
,長(zhǎng)軸在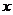 軸上,上頂點(diǎn)為
軸上,上頂點(diǎn)為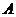 ,左、右焦點(diǎn)分別為
,左、右焦點(diǎn)分別為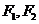 ,線段
,線段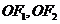 的中點(diǎn)分別為
的中點(diǎn)分別為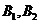 ,且△
,且△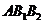 是面積為4的直角三角形。(Ⅰ)求該橢圓的離心率和標(biāo)準(zhǔn)方程;(Ⅱ)過(guò)
是面積為4的直角三角形。(Ⅰ)求該橢圓的離心率和標(biāo)準(zhǔn)方程;(Ⅱ)過(guò)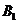 作直線交橢圓于
作直線交橢圓于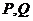 ,
,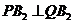 ,求△
,求△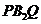 的面積
的面積
【答案】:(Ⅰ)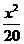 +
+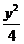 =1(Ⅱ)
=1(Ⅱ)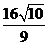
 ,
,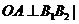
 (*)
(*)
設(shè)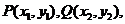 則
則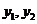 是上面方程的兩根,因此
是上面方程的兩根,因此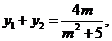
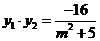 又
又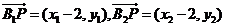 ,所以
,所以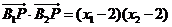
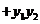
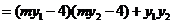
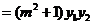
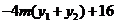
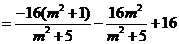
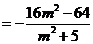 由
由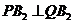 ,知
,知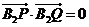 ,即
,即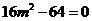 ,解得
,解得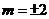
當(dāng)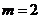 時(shí),方程(*)化為:
時(shí),方程(*)化為: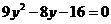
故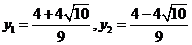 ,
,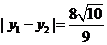
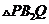 的面積
的面積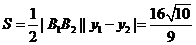 當(dāng)
當(dāng)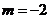 時(shí),同理可得(或由對(duì)稱性可得)
時(shí),同理可得(或由對(duì)稱性可得)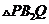 的面積
的面積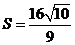 綜上所述,
綜上所述,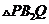 的面積為
的面積為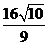 。
。











