二、填空題:本大題共5小題,每小題5分,共25分,把答案填在答題卡的相應(yīng)位置。
(11)首項(xiàng)為1,公比為2的等比數(shù)列的前4項(xiàng)和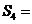
【答案】:15
【解析】: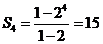
【考點(diǎn)定位】本題考查等比數(shù)列的前n項(xiàng)和公式
(12)函數(shù)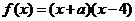 為偶函數(shù),則實(shí)數(shù)
為偶函數(shù),則實(shí)數(shù)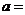

(13)設(shè)△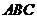 的內(nèi)角
的內(nèi)角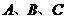 的對(duì)邊分別為
的對(duì)邊分別為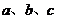 ,且
,且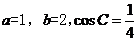 ,則
,則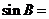
【答案】: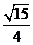

(14)設(shè)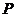 為直線
為直線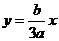 與雙曲線
與雙曲線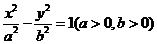 左支的交點(diǎn),
左支的交點(diǎn),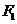 是左焦點(diǎn),
是左焦點(diǎn),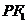 垂直于
垂直于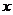 軸,則雙曲線的離心率
軸,則雙曲線的離心率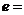

(15)某藝校在一天的6節(jié)課中隨機(jī)安排語(yǔ)文、數(shù)學(xué)、外語(yǔ)三門文化課和其它三門藝術(shù)課各1節(jié),則在課表上的相鄰兩節(jié)文化課之間至少間隔1節(jié)藝術(shù)課的概率為 (用數(shù)字作答)。
【答案】: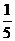

三、解答題:本大題共6小題,共75分。解答應(yīng)寫出文字說(shuō)明、證明過(guò)程或演算步驟。
16.(本小題滿分13分,(Ⅰ)小問(wèn)6分,(Ⅱ)小問(wèn)7分))已知
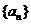 為等差數(shù)列,且
為等差數(shù)列,且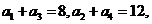 (Ⅰ)求數(shù)列
(Ⅰ)求數(shù)列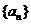 的通項(xiàng)公式;(Ⅱ)記
的通項(xiàng)公式;(Ⅱ)記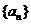 的前
的前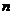 項(xiàng)和為
項(xiàng)和為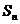 ,若
,若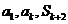 成等比數(shù)列,求正整數(shù)
成等比數(shù)列,求正整數(shù)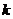 的值。
的值。
【答案】:(Ⅰ)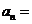
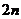 (Ⅱ)
(Ⅱ)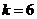
【解析】::(Ⅰ)設(shè)數(shù)列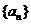 的公差為d,由題意知
的公差為d,由題意知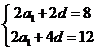 解得
解得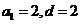
所以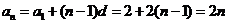
(Ⅱ)由(Ⅰ)可得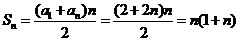 因
因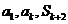 成等比數(shù)列,所以
成等比數(shù)列,所以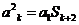 從而
從而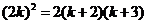 ,即
,即 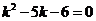
解得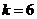 或
或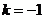 (舍去),因此
(舍去),因此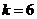 。
。
17.(本小題滿分13分)已知函數(shù)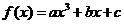 在
在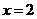 處取得極值為
處取得極值為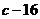
(1)求a、b的值;(2)若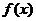 有極大值28,求
有極大值28,求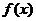 在
在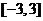 上的最大值.
上的最大值.
【答案】:(Ⅰ)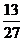 (Ⅱ)
(Ⅱ)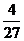
【解析】::(Ⅰ)因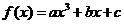 故
故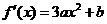 由于
由于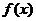 在點(diǎn)
在點(diǎn)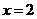 處取得極值
處取得極值
故有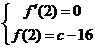 即
即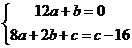 ,化簡(jiǎn)得
,化簡(jiǎn)得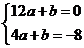 解得
解得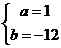
(Ⅱ)由(Ⅰ)知 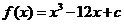 ,
,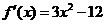
令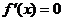 ,得
,得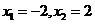 當(dāng)
當(dāng)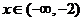 時(shí),
時(shí),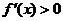 故
故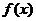 在
在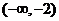 上為增函數(shù);
上為增函數(shù);
當(dāng)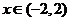 時(shí),
時(shí),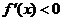 故
故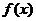 在
在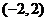 上為減函數(shù)
上為減函數(shù)
當(dāng)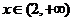 時(shí)
時(shí)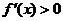 ,故
,故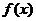 在
在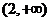 上為增函數(shù)。
上為增函數(shù)。
由此可知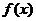 在
在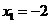 處取得極大值
處取得極大值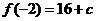 ,
,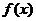 在
在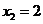 處取得極小值
處取得極小值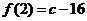 由題設(shè)條件知
由題設(shè)條件知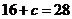 得
得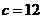 此時(shí)
此時(shí)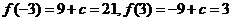 ,
,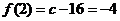 因此
因此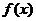 上
上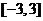 的最小值為
的最小值為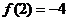
【考點(diǎn)定位】本題主要考查函數(shù)的導(dǎo)數(shù)與極值,最值之間的關(guān)系,屬于導(dǎo)數(shù)的應(yīng)用.(1)先對(duì)函數(shù)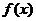 進(jìn)行求導(dǎo),根據(jù)
進(jìn)行求導(dǎo),根據(jù)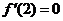 =0,
=0,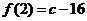 ,求出a,b的值.(1)根據(jù)函數(shù)
,求出a,b的值.(1)根據(jù)函數(shù)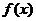 =x3-3ax2+2bx在x=1處有極小值-1先求出函數(shù)中的參數(shù)a,b的值,再令導(dǎo)數(shù)等于0,求出極值點(diǎn),判斷極值點(diǎn)左右兩側(cè)導(dǎo)數(shù)的正負(fù),當(dāng)左正右負(fù)時(shí)有極大值,當(dāng)左負(fù)右正時(shí)有極小值.再代入原函數(shù)求出極大值和極小值.(2)列表比較函數(shù)的極值與端點(diǎn)函數(shù)值的大小,端點(diǎn)函數(shù)值與極大值中最大的為函數(shù)的最大值,端點(diǎn)函數(shù)值與極小值中最小的為函數(shù)的最小值.
=x3-3ax2+2bx在x=1處有極小值-1先求出函數(shù)中的參數(shù)a,b的值,再令導(dǎo)數(shù)等于0,求出極值點(diǎn),判斷極值點(diǎn)左右兩側(cè)導(dǎo)數(shù)的正負(fù),當(dāng)左正右負(fù)時(shí)有極大值,當(dāng)左負(fù)右正時(shí)有極小值.再代入原函數(shù)求出極大值和極小值.(2)列表比較函數(shù)的極值與端點(diǎn)函數(shù)值的大小,端點(diǎn)函數(shù)值與極大值中最大的為函數(shù)的最大值,端點(diǎn)函數(shù)值與極小值中最小的為函數(shù)的最小值.











