評(píng)論
打印
第Ⅱ卷
本卷包括必考題和選考題兩部分。第13題~第21題為必考題，每個(gè)試題考生都必須作答。第22題~第24題為選考題，考生根據(jù)要求作答。
二．填空題：本大題共4小題，每小題5分。
（15）Sn為等差數(shù)列{an}的前n項(xiàng)和，S2=S6，a4=1，則a5=____________。
答案： -1
解析：設(shè)等差數(shù)列的公差為d，解方程組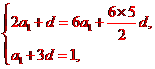
得d=-2，a5=a4+d=-1.
（16）已知函數(shù)f（x）=ex-2x+a有零點(diǎn)，則a的取值范圍是___________。
答案：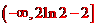 
解析：函數(shù)f（x）=ex-2x+a有零點(diǎn)，即方程f（x）=0有解，即-a =ex-2x有解，設(shè)g(x)= ex-2x,
因?yàn)間’(x)= ex-2,當(dāng)x>ln2時(shí)g’(x)>0, 當(dāng)x<ln2時(shí)g’(x)<0,所以函數(shù)g(x)有最小值，最小值就是極小值g(ln2)=2-2ln2，由-a≥2-2ln2，得a的取值范圍。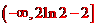
三、解答題：解答應(yīng)寫文字說明，證明過程或演算步驟。
（18）（本小題滿分12分）
如圖，四邊形ABCD為正方形，QA⊥平面ABCD，PD∥QA，QA=AB=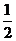
PD。
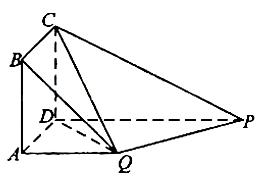
（I）證明：PQ⊥平面DCQ；
（II）求棱錐Q-ABCD的體積與棱錐P-DCQ的體積的比值。
解析：（I）由條件知，PDAQ是直角梯形，
因?yàn)锳Q⊥平面ABCD,所以平面PDAQ⊥平面ABCD,交線是AD。
又四邊形ABCD是正方形，DC⊥AD,所以DC⊥平面PDAQ，可得PQ⊥DC。
在直角梯形PDAQ中可得DQ=PQ=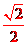
PD，則PQ⊥QD.
所以PQ⊥平面PCQ.
分別求品種甲和品種乙的每公頃產(chǎn)量的樣本平均數(shù)和樣本方差；根據(jù)試驗(yàn)結(jié)果，你認(rèn)為應(yīng)該種植哪一品種？
附：
樣本數(shù)據(jù)x1，x2，…，xa的樣本方差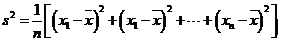
，其中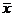
為樣本平均數(shù)。
，
，
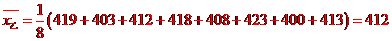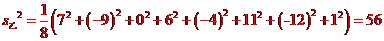由以上結(jié)果可以看出，品種乙的樣本平均數(shù)大于品種甲的樣本平均數(shù)，且兩品種的樣本方差差異不大，故應(yīng)該選擇種植品種乙。
