二、選擇題(本大題共有4小題,滿分20分)每題有且只有一個正確答案,考生應在答題紙的相應編號上,將代表答案的小方格涂黑,選對得5分,否則一律得零分.
15.函數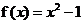 (x≥0)的反函數為f -1(x),則f -1(2)的值是( A )
(x≥0)的反函數為f -1(x),則f -1(2)的值是( A )
(A)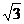 (B)-
(B)-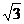 (C)1+
(C)1+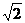 (D)1-
(D)1-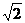
【答案】 A
【解析】 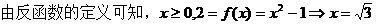
選A
16.設常數a∈R,集合A=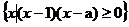 ,B=
,B=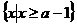 .若A∪B=R,則a的取值范圍為( B )
.若A∪B=R,則a的取值范圍為( B )
(A)(-∞,2) (B)(-∞,2] (C)(2,+∞) (D)[2,+∞)
【答案】 B
【解析】 方法:代值法,排除法。當a=1時,A=R,符合題意;當a=2時,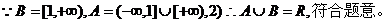
綜上,選B
標準解法如下: 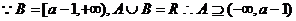
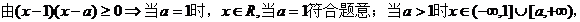
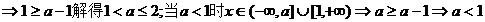 .
.
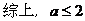
選B
17.錢大姐常說“好貨不便宜”,她這句話的意思是:“好貨”是“不便宜”的( A )
(A)充分條件 (B)必要條件
(C)充分必要條件 (D)既非充分又非必要條件
【答案】 A
【解析】 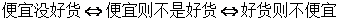
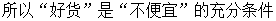
選A
當點(x,y)分別在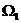 ,
,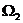 ,…上時,x+y的最大值分別是M1,M2,…,則
,…上時,x+y的最大值分別是M1,M2,…,則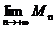 =( D )
=( D )
(A)0 (B)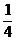 (C)2 (D)
(C)2 (D)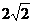
【答案】 D
【解析】 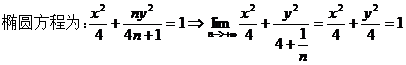
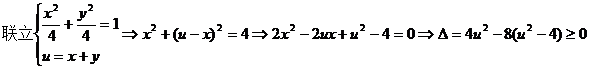
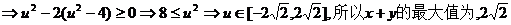
選D
三、解答題(本大題共有5下題,滿分74分)解答下列各題必須在答題紙相應編號的規定區域內寫出必要的步驟.
19.(本題滿分12分)
如圖,正三棱錐O-ABC的底面邊長為2,高為1,求該三棱錐的體積及表面積。
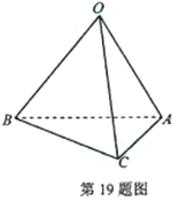
【答案】 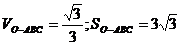
【解析】 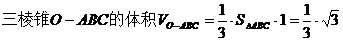
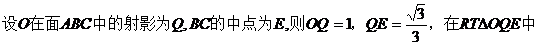
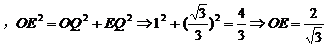
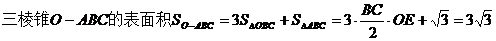
所以,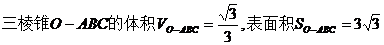
20.(本題滿分14分)本題共有2個小題,第1小題滿分5分,第2小題滿分9分.
甲廠以x千克/小時的速度勻速生產某種產品(生產條件要求1≤x≤10),每小時可獲得的利潤是100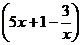 元.
元.
(1)求證:生產a千克該產品所獲得的利潤為100a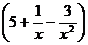 元;
元;
(2)要使生產900千克該產品獲得的利潤最大,問:甲廠應該選取何種生產速度?并求此最大利潤.
【答案】 (1) 見下
(2)當生產速度為6千克/小時,這時獲得最大利潤為457500元。
【解析】 (1)證明:由題知,生產a千克該產品所需要的時間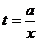 小時,
小時,
所獲得的利潤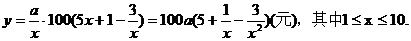
所以,生產a千克該產品所獲得的利潤為100a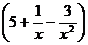 元;(證畢)
元;(證畢)
(2) 由(1)知,生產900千克該產品即a=900千克時,獲得的利潤
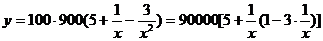
由二次函數的知識可知,當 =
=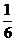 ,即x=6時,
,即x=6時,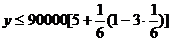
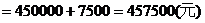
所以,當生產速度為6千克/小時,這時獲得最大利潤為457500元。
21.(本題滿分14分)本題共有2個小題,第1小題滿分6分,第2小題滿分8分.
已知函數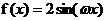 ,其中常數ω>0.
,其中常數ω>0.
(1)令ω=1,判斷函數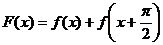 的奇偶性,并說明理由;
的奇偶性,并說明理由;
(2)令ω=2,將函數y=f(x)的圖像向左平移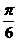 個單位,再向上平移1個單位,得到函數y=g(x)的圖像.對任意a∈R,求y=g(x)在區間[a,a+10π]上零點個數的所有可能值.
個單位,再向上平移1個單位,得到函數y=g(x)的圖像.對任意a∈R,求y=g(x)在區間[a,a+10π]上零點個數的所有可能值.
【答案】 (1) 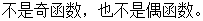
(2) 20,21
【解析】 (1)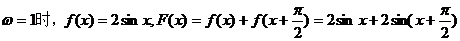
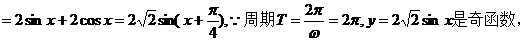
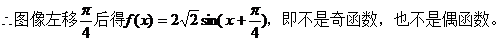
(2)ω=2,將函數y=f(x)的圖像向左平移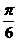 個單位,再向上平移1個單位,得到函數y=g(x):
個單位,再向上平移1個單位,得到函數y=g(x):
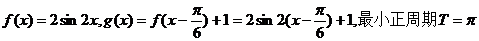 .
.

所以y=g(x)在區間[a, a+10π]、其長度為10個周期上,零點個數可以取20,21個
22.(本題滿分16分)本題共有3個小題,第1小題滿分3分,第2小題滿分5分,第3小題滿分8分.
已知函數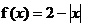 ,無窮數列
,無窮數列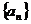 滿足an+1=f(an),n∈N*
滿足an+1=f(an),n∈N*
(1)若a1=0,求a2,a3,a4;
(2)若a1>0,且a1,a2,a3成等比數列,求a1的值.
(3)是否存在a1,使得a1,a2,…,an…成等差數列?若存在,求出所有這樣的a1;若不存在,說明理由.
【答案】 (1) 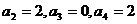
(2)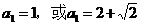
(3)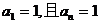
【解析】 (1) 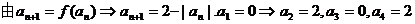
(2)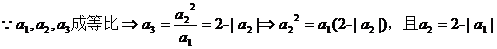
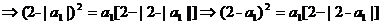
分情況討論如何:
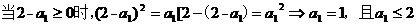
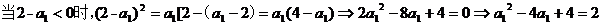
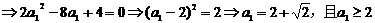

(3)
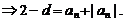 討論如下:
討論如下:
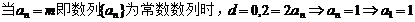
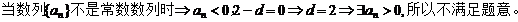
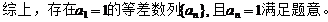
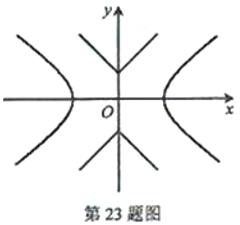
23.(本題滿分18分)本題共有3個小題,第1小題滿分3分,第2小題滿分6分,第3小題滿分9分.
如圖,已知雙曲線C1: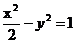 ,曲線C2:
,曲線C2: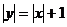 .P是平面內一點.若存在過點P的直線與C1、C2都有共同點,則稱P為“C1-C2型點”.
.P是平面內一點.若存在過點P的直線與C1、C2都有共同點,則稱P為“C1-C2型點”.
(1)在正確證明C1的左焦點是“C1-C2型點”時,要使用一條過該焦點的直線,試寫出一條這樣的直線的方程(不要求驗證);
(2)設直線y=kx與C2有公共點,求證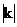 >1,進而證明圓點不是“C1-C2型點”;
>1,進而證明圓點不是“C1-C2型點”;
(3)求證:圓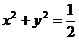 內的點都不是“C1-C2型點”.
內的點都不是“C1-C2型點”.
【答案】 (1) 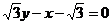
【解析】 (1) 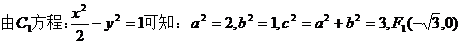 顯然,由雙曲線
顯然,由雙曲線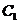 的幾何圖像性質可知,過
的幾何圖像性質可知,過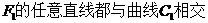 .從曲線
.從曲線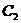 圖像上取點P(0,1),則直線
圖像上取點P(0,1),則直線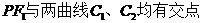 。這時直線方程為
。這時直線方程為
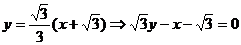
(2) 先證明“若直線y=kx與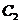 有公共點,則
有公共點,則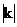 >1”.
>1”.
雙曲線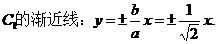
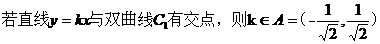 .
.
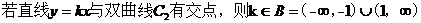 .
.
所以直線y=kx與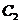 有公共點,則
有公共點,則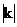 >1 . (證畢)
>1 . (證畢)
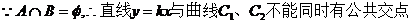 。
。
所以原點不是“C1-C2型點”;(完)
(3)設直線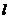 過圓
過圓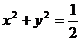 內一點,則直線
內一點,則直線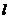 斜率不存在時與曲線
斜率不存在時與曲線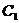 無交點。
無交點。
設直線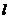 方程為:y = kx + m,則:
方程為:y = kx + m,則: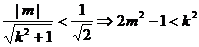
假設直線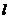 與曲線
與曲線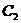 相交上方,則
相交上方,則