(17)(本小題滿分13分,(Ⅰ)小問9分,(Ⅱ)、(Ⅲ)小問各2分)
從某居民區隨機抽取10個家庭,獲得第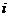 個家庭的月收入
個家庭的月收入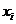 (單位:千元)與月儲蓄
(單位:千元)與月儲蓄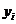 (單位:千元)的數據資料,算得
(單位:千元)的數據資料,算得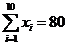 ,
,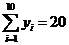 ,
,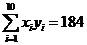 ,
,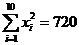 .
.
(Ⅰ)求家庭的月儲蓄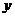 對月收入
對月收入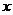 的線性回歸方程
的線性回歸方程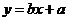 ;
;
(Ⅱ)判斷變量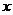 與
與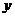 之間是正相關還是負相關;
之間是正相關還是負相關;
(Ⅲ)若該居民區某家庭月收入為7千元,預測該家庭的月儲蓄.
附:線性回歸方程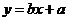 中,
中,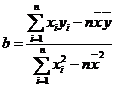 ,
,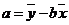 ,
,
其中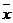 ,
,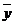 為樣本平均值,線性回歸方程也可寫為
為樣本平均值,線性回歸方程也可寫為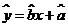 .
.


(18)(本小題滿分13分,(Ⅰ)小問4分,(Ⅱ)小問9分)
在△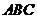 中,內角
中,內角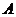 、
、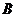 、
、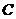 的對邊分別是
的對邊分別是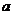 、
、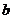 、
、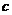 ,且
,且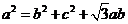 .
.
(Ⅰ)求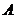 ;
;
(Ⅱ)設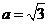 ,
,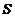 為△
為△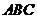 的面積,求
的面積,求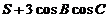 的最大值,并指出此時
的最大值,并指出此時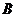 的值.
的值.

(19)(本小題滿分12分,(Ⅰ)小問5分,(Ⅱ)小問7分)
如題(19)圖,四棱錐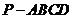 中,
中,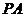 ⊥底面
⊥底面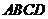 ,
,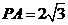 ,
,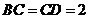 ,
, 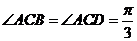 .
.
(Ⅰ)求證: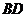 ⊥平面
⊥平面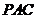 ;
;
(Ⅱ)若側棱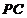 上的點
上的點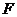 滿足
滿足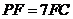 ,求三棱錐
,求三棱錐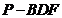 的體積.
的體積.


(20)(本小題滿分12分,(Ⅰ)小問5分,(Ⅱ)小問7分)
某村莊擬修建一個無蓋的圓柱形蓄水池(不計厚度).設該蓄水池的底面半徑為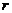 米,高為
米,高為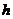 米,體積為
米,體積為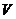 立方米.假設建造成本僅與表面積有關,側面積的建造成本為100元/平方米,底面的建造成本為160元/平方米,該蓄水池的總建造成本為12000
立方米.假設建造成本僅與表面積有關,側面積的建造成本為100元/平方米,底面的建造成本為160元/平方米,該蓄水池的總建造成本為12000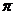 元(
元(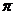 為圓周率).
為圓周率).
(Ⅰ)將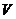 表示成
表示成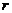 的函數
的函數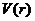 ,并求該函數的定義域;
,并求該函數的定義域;
(Ⅱ)討論函數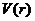 的單調性,并確定
的單調性,并確定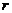 和
和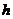 為何值時該蓄水池的體積最大.
為何值時該蓄水池的體積最大.


(21)(本小題滿分12分,(Ⅰ)小問4分,(Ⅱ)小問8分)
如題(21)圖,橢圓的中心為原點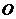 ,長軸在
,長軸在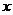 軸上,離心率
軸上,離心率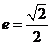 ,過左焦點
,過左焦點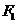 作
作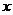 軸的垂線交橢圓于
軸的垂線交橢圓于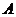 、
、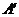 兩點,
兩點,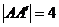 .
.
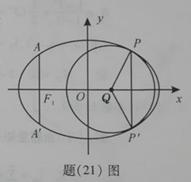
(Ⅰ)求該橢圓的標準方程;
(Ⅱ)取平行于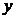 軸的直線與橢圓相較于不同的兩點
軸的直線與橢圓相較于不同的兩點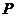 、
、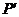 ,過
,過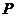 、
、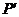 作圓心為
作圓心為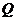 的圓,使橢圓上的其余點均在圓
的圓,使橢圓上的其余點均在圓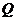 外.求
外.求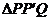 的面積
的面積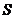 的最大值,并寫出對應的圓
的最大值,并寫出對應的圓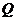 的標準方程.
的標準方程.














