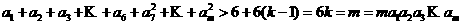(19)(本小題12分)
解法一:
(Ⅰ)因?yàn)锳D//BC,且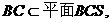 所以
所以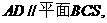 從而A點(diǎn)到平面
從而A點(diǎn)到平面 的距離等于D點(diǎn)到平面
的距離等于D點(diǎn)到平面 的距離。
的距離。
因?yàn)槠矫?img onmouseover='upNext(this)' title="1410428131976764.gif" src="http://pic.kekenet.com/2014/0911/1410430145988367.gif"/>故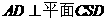 ,從而
,從而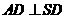 ,由AD//BC,得
,由AD//BC,得
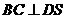 ,又由
,又由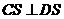 知
知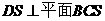 ,從而
,從而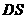 為點(diǎn)A到平面
為點(diǎn)A到平面 的距離,因此在
的距離,因此在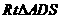 中
中
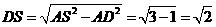
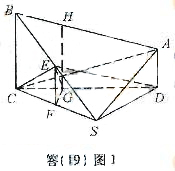
(Ⅱ)如答(19)圖1,過E電作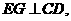 交
交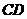 于點(diǎn)G,又過G點(diǎn)作
于點(diǎn)G,又過G點(diǎn)作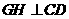 ,交AB于H,故
,交AB于H,故
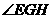 為二面角
為二面角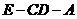 的平面角,記為
的平面角,記為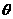 ,過E點(diǎn)作EF//BC,交
,過E點(diǎn)作EF//BC,交 于點(diǎn)F,連結(jié)GF,因平面
于點(diǎn)F,連結(jié)GF,因平面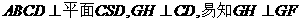 ,故
,故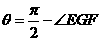 .
.
由于E為BS邊中點(diǎn),故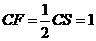 ,在
,在 中,
中,
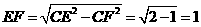 ,因
,因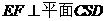 ,又
,又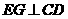
故由三垂線定理的逆定理得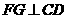 ,從而又可得
,從而又可得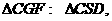
因此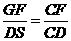 而在
而在 中,
中,
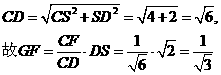
在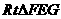 中,
中,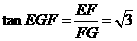 可得
可得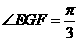 ,故所求二面角的大小為
,故所求二面角的大小為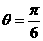
解法二:
(Ⅰ)如答(19)圖2,以S(O)為坐標(biāo)原點(diǎn),射線OD,OC分別為x軸,y軸正向,建立空間坐標(biāo)系,設(shè)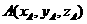 ,因平面
,因平面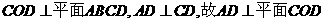
即點(diǎn)A在xoz平面上,因此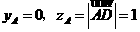
又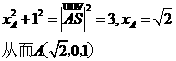
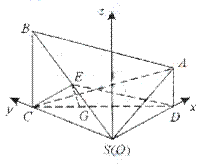
因AD//BC,故BC⊥平面CSD,即BCS與平面
yOx重合,從而點(diǎn)A到平面BCS的距離為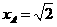 .
.
(Ⅱ)易知C(0,2,0),D(,0,0). 因E為BS的中點(diǎn).
ΔBCS為直角三角形 ,
知 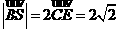
設(shè)B(0,2, 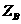 ),
),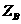 >0,則
>0,則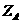 =2,故B(0,2,2),所以E(0,1,1) .
=2,故B(0,2,2),所以E(0,1,1) .
在CD上取點(diǎn)G,設(shè)G(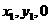 ),使GE⊥CD .
),使GE⊥CD .
由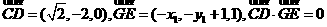 故
故
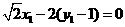 ①
①
又點(diǎn)G在直線CD上,即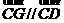 ,由
,由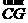 =(
=(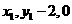 ),則有
),則有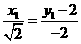 ②
②
聯(lián)立①、②,解得G=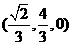 ,
,
故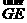 =
=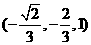 .又由AD⊥CD,所以二面角E-CD-A的平面角為向量
.又由AD⊥CD,所以二面角E-CD-A的平面角為向量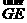 與向量
與向量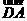 所成的角,記此角為
所成的角,記此角為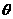 .
.
因?yàn)?img onmouseover='upNext(this)' title="1410428297269667.gif" src="http://pic.kekenet.com/2014/0911/1410430155307557.gif"/>=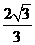 ,
,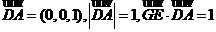 ,所以
,所以
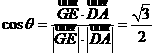
故所求的二面角的大小為 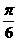 .
.
(20)(本小題12分)
解:(Ⅰ)由題設(shè)條件知焦點(diǎn)在y軸上,故設(shè)橢圓方程為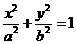 (a >b> 0 ).
(a >b> 0 ).
設(shè)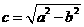 ,由準(zhǔn)線方程
,由準(zhǔn)線方程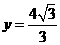 得.由
得.由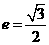 得
得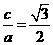 ,解得 a = 2 ,c =
,解得 a = 2 ,c = 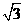 ,從而 b = 1,橢圓方程為
,從而 b = 1,橢圓方程為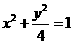 .
.
又易知C,D兩點(diǎn)是橢圓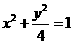 的焦點(diǎn),所以,
的焦點(diǎn),所以,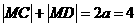
從而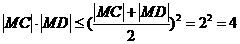 ,當(dāng)且僅當(dāng)
,當(dāng)且僅當(dāng)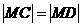 ,即點(diǎn)M的坐標(biāo)為
,即點(diǎn)M的坐標(biāo)為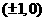 時(shí)上式取等號(hào),
時(shí)上式取等號(hào),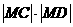 的最大值為4 .
的最大值為4 .
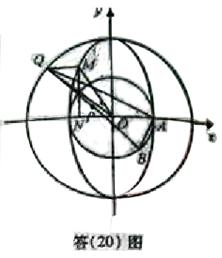
(II)如圖(20)圖,設(shè)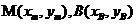
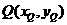 .因?yàn)?img onmouseover='upNext(this)' title="1410428350156950.gif" src="http://pic.kekenet.com/2014/0911/1410430156968404.gif"/>,故
.因?yàn)?img onmouseover='upNext(this)' title="1410428350156950.gif" src="http://pic.kekenet.com/2014/0911/1410430156968404.gif"/>,故
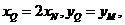
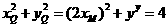 ①
①
因?yàn)?img onmouseover='upNext(this)' title="1410428351765718.gif" src="http://pic.kekenet.com/2014/0911/1410430156818126.gif"/>
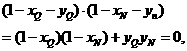
所以 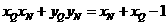 . ②
. ②
記P點(diǎn)的坐標(biāo)為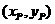 ,因?yàn)镻是BQ的中點(diǎn)
,因?yàn)镻是BQ的中點(diǎn)
所以 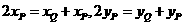
由因?yàn)? 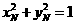 ,結(jié)合①,②得
,結(jié)合①,②得
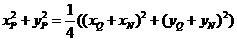
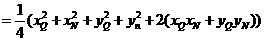
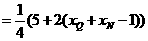
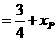
故動(dòng)點(diǎn)P的估計(jì)方程為
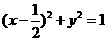
(21)(本小題12分)
解:(I)因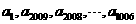 是公比為d的等比數(shù)列,從而
是公比為d的等比數(shù)列,從而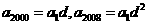 由
由 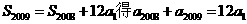 ,故
,故
解得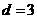 或
或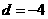 (舍去)。因此
(舍去)。因此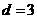
又 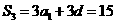 。解得
。解得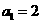
從而當(dāng)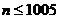 時(shí),
時(shí),
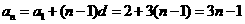
當(dāng)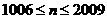 時(shí),由
時(shí),由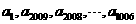 是公比為d的等比數(shù)列得
是公比為d的等比數(shù)列得
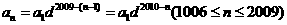
因此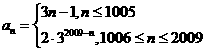
(II)由題意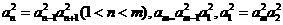 得
得
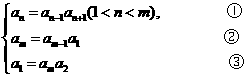
有①得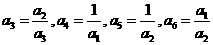 ④
④
由①,②,③得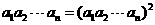 ,
,
故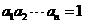 . ⑤
. ⑤
又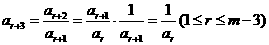 ,故有
,故有
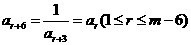 .⑥
.⑥
下面反證法證明: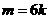
若不然,設(shè)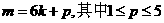
若取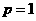 即
即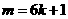 ,則由⑥得
,則由⑥得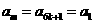 ,而由③得
,而由③得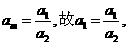
得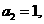 由②得
由②得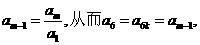 而
而
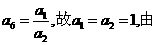 ④及⑥可推得
④及⑥可推得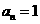 (
(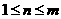 )與題設(shè)矛盾
)與題設(shè)矛盾
同理若P=2,3,4,5均可得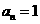 (
(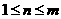 )與題設(shè)矛盾,因此
)與題設(shè)矛盾,因此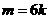 為6的倍數(shù)
為6的倍數(shù)
由均值不等式得
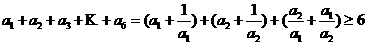
由上面三組數(shù)內(nèi)必有一組不相等(否則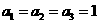 ,從而
,從而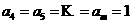 與題設(shè)矛盾),故等號(hào)不成立,從而
與題設(shè)矛盾),故等號(hào)不成立,從而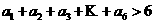
 又
又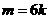 ,由④和⑥得
,由④和⑥得
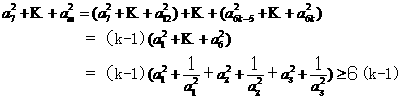
因此由⑤得