X squared plus y squared equals zee squared, and you can ask:
X^2+y^2=z^2,你可以問:
well what are the whole numbers solutions of this equation?
那么這個等式的整數解是什么?
And you quickly find there's a solution 3 squared plus 4 squared equals 5 squared.
你很快就會找到一個答案是3^2+4^2=5^2。
Another one is 5 squared plus 12 squared is 13 squared, and you go on looking and you find more and more.
另個答案是5^2+12^2=13^2,繼續尋找,你會找到越來越多的整數解。
So then a natural question is, the question Fermat raised:
一個自然而然的問題,也是費馬提出的問題是:
supposing you change from squares, supposing you replace the two by three, by four, by five, by six, by any whole number 'n',
假設改變次方數,假設將平方改為三次方、四次方、五次方、六次方,以及任何整數'n'次方,
and Fermat said simply that you'll never find any solutions,
費馬說僅如此,你就找不到任何解,
however far you look you'll never find a solution.
不管你怎么找,你永遠也找不到一個解。
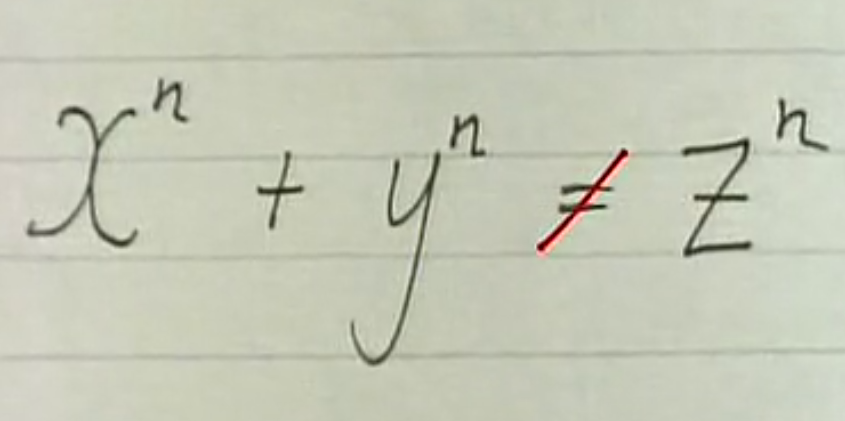
You will never find numbers that fit this equation, if n is greater than 2.
如果n大于2,你永遠也找不到符合這個等式的數字。
That's what Fermat said, and what's more, he said he could prove it.
那正是費馬所聲稱的,此外,他說他可以對之進行證明。
In a moment of brilliance, he scribbled the following mysterious note.
靈智閃現之時,他寫下了如下神秘的話語。
Written in Latin, he says he has a truly wonderful proof "Demonstrationem mirabilem" of this fact,
他用拉丁文寫道,關于這一事實他有了一個確實了不起的證明,"Demonstrationem mirabilem",
and then the last words are: "Hanc marginis exigiutas non caperet", this margin is too small to contain this.
他最后語句是: "Hanc marginis exigiutas non caperet",這空白處太小了,寫不下。
So Fermat said he had a proof, but he never said what it was.
因此費馬說他有個證明,但他從沒有說出來那是什么。











