Pierre de Fermat was a 17th-century French mathematician who made some of the greatest breakthroughs in the history of numbers.
皮埃爾·德·費馬是17世紀時期的法國數學家,他在數學歷史上成就了一些最偉大的突破。
His inspiration came from studying the Arithmetica, that Ancient Greek text.
他的靈感來自于研習"算術"那本古希臘著作。
Fermat owned a copy of this book, which is a book about numbers with lots of problems, which presumably Fermat tried to solve.
費馬有這本書的一份復本,這本書是關于數字以及許多難題,是費馬力圖解決的那些。
He studied it, he wrote notes in the margins.
他研習它,在空欄處寫下筆記。
Fermat's original notes were lost, but they can still be read in a book published by his son.
費馬的原始筆記已遺失,但在他兒子出版的書中可看到那些。
It was one of these notes that was Fermat's greatest legacy.
這些筆記中的一條正是費馬最偉大的遺產。
And this is the fantastic observation of Master Pierre de Fermat which caused all the trouble: "Cubum autem in duos cubos"
皮埃爾·德·費馬大人的這個奇妙觀察成果惹出了所有的麻煩:"Cubum autem in duos cubos"。
This tiny note is the world's hardest mathematical problem.
這條短短的手記是世界上最困難的數學題。
It's been unsolved for centuries, yet it begins with an equation so simple that children know it off by heart.
數世紀以來未獲破解,它起始于一個等式,簡單得孩子們早已銘記于心。
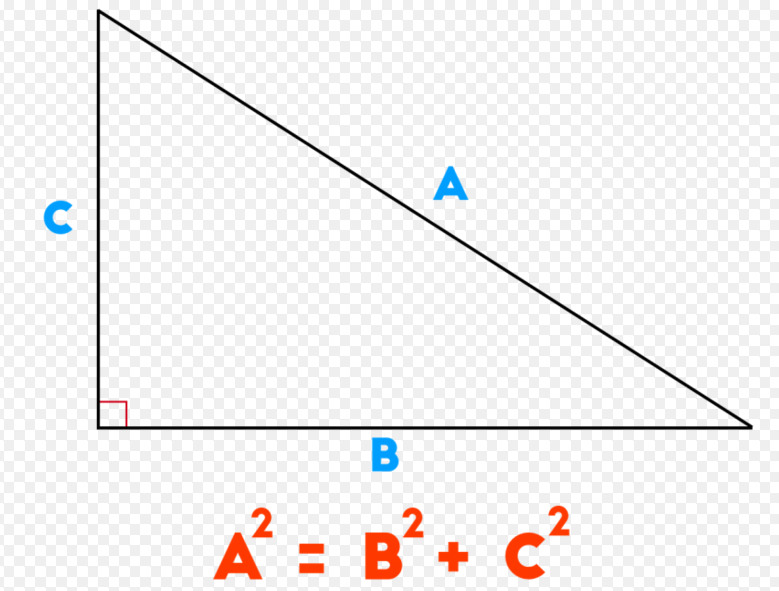
The square of the hypotenuse is equal to the sum of the squares of the other two sides.
直角三角形斜邊的平方等于另兩邊平方之和。
Yes well that's Pythagoras's theorem isn't it, that's what we all did at school.
那就是勾股定理,不是嗎,那正是我們在學校里都用過的。
So Pythagoras's theorem, the clever thing about it is that it tells us
對于勾股定理,其奇妙之處在于告訴了我們,
when three numbers are the sides of a right-angle triangle, that happens just when x squared plus y squared equals z squared.
當三個數字是個直角三角形的三條邊時,x的平方+y的平方=z的平方時,就是那樣。












