Taniyama-Shimura went on to become one of the great unproven conjectures.
谷山-志村猜想仍舊是一個未經驗證的大猜想。
But what did it have to do with Fermat's last theorem?
但它和費馬最后定理間有什么關系?
At that time no-one had any idea that Taniyama-Shimura could have anything to do with Fermat.
那時沒人會想到谷山-志村猜想會和費馬有什么關聯。
Of course in the '80s that all changed completely.
當然到了80年代,一切都完全變了。
Taniyama-Shimura says: every elliptic curve is modular and Fermat says: no numbers fit this equation.
谷山-志村猜想說:每條橢圓曲線都是模;而費馬說:沒有滿足這個等式的數。
What was the connection?
其關聯是什么?
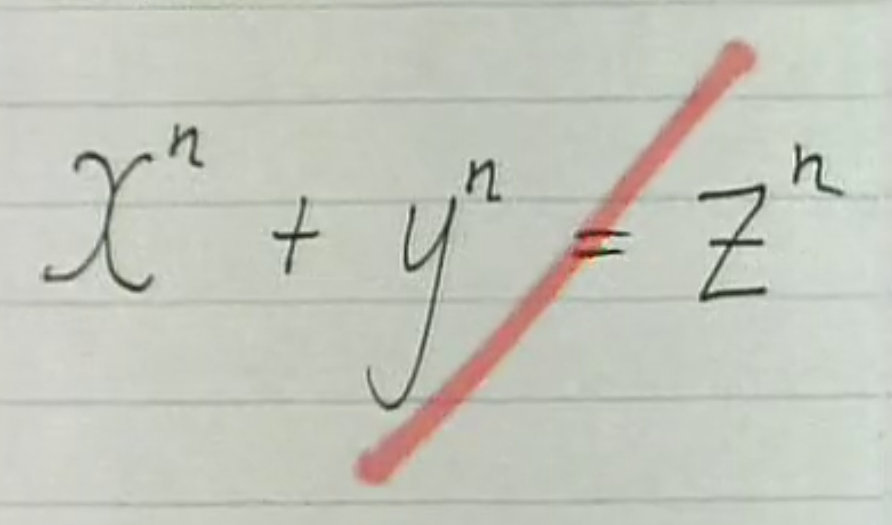
Well, on the face of it the Shimura-Taniyama conjecture which is about elliptic curves,
表面上看來,谷山-志村猜想是關于橢圓曲線的,
and Fermat's last theorem have nothing to do with each other
而費馬最后定理與它沒有關系,
because there's no connection between Fermat and elliptic curves.
因為費馬和橢圓曲線之間沒有關聯。
But in 1985 Gerhard Frey had this amazing idea.
但在1985年,格爾哈德·弗萊有了這個了不起的想法。
Frey, a German mathematician, considered the unthinkable:
弗萊,一個德國數學家,考慮的是不可想象的可能:
what would happen if Fermat was wrong and there was a solution to this equation after all?
如果費馬有誤,這個等式根本就有解的話會如何呢?











