SAT數(shù)學(xué)雖然簡單，也需要我們努力備考。下面天道小編為大家具體介紹SAT數(shù)學(xué)分析：Lines and Distance，希望對大家備考SAT數(shù)學(xué)考試有所幫助。

SAT(Scholastic Assessment Test)是美國高中生進入美國大學(xué)需要參加的考試，也就是美國的“高考”。近年來，越來越多的準備去美國讀本科的中國高中生開始參加SAT的考試。

Lines and distance are fundamental to coordinate geometry, not to mention to the Math IC test. Even the most complicated coordinate geometry question uses the concepts covered in the next few sections.

DistanceMeasuring distance in the coordinate plane is made possible thanks to the Pythagorean theorem. If you are given two points, (x1,y1), and (x2,y2), their distance from each other is given by the following formula:

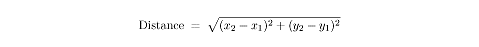
The diagram below shows how the Pythagorean theorem plays a role in the formula. The distance between two points can be represented by the hypotenuse of a right triangle whose legs are lengths (x2 – x1) and (y2 – y1).

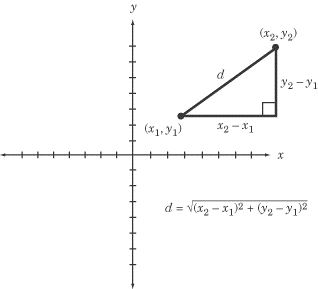
To calculate the distance from (4, –3) to (–3, 8), plug the coordinates into the formula:The distance between the points is , which equals approximately 13.04. You can double-check this answer by plugging it back into the Pythgorean theorem.Finding MidpointsThe midpoint between two points in the coordinate plane can be calculated using a formula. If the endpoints of a line segment are (x1, y1) and (x2, y2), then the midpoint of the line segment is:In other words, the x- and y-coordinates of the midpoint are the averages of the x- and y-coordinates of the endpoints.Here’s a practice question:What is the midpoint of the line segment whose endpoints are (6, 0) and (3, 7)?To solve, all you need to do is plug the points given into the midpoint formula . x1 = 6, y1 = 0, x2 = 3, and y2 = 7:

以上便是SAT數(shù)學(xué)分析：Lines and Distance的介紹，非常詳細，希望對大家有所幫助，各位考生可以根據(jù)自己的具體情況有選擇地進行借鑒，天道小編祝大家都能取得理想的SAT數(shù)學(xué)考試成績!