下面為大家整理的是4道SAT數學練習題的內容,后面都附有詳細的答案解析。SAT數學考試是非常注重對考生實際運用知識點能力的考察的,所以大家在備考的時候,一定要多加練習才行。下面我們來看看詳細內容吧。
Read the following SAT test question and then click on a button to select your answer.
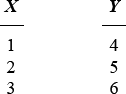
1.If x is a number from Column x and y is a number from Column y in the table above, how many different values are possible for x+y?
(A) Nine
(B) Eight
(C) Seven
(D) Six
(E) Five
Read the following SAT test question and then click on a button to select your answer.
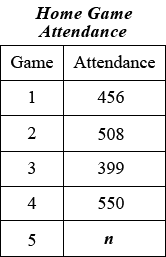
2.The table above shows the attendance at the home games of the Central High School football team. If the median attendance for the five games was 456, and no two games had the same attendance, what is the greatest possible value for n?
(A) 400
(B) 455
(C) 457
(D) 478
(E) 549
Read the following SAT test question and then click on a button to select your answer.
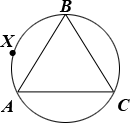
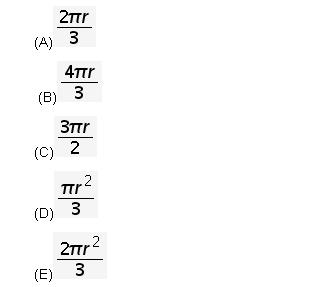
3.In the figure above, inscribed triangle ABC is equilateral. If the radius of the circle is r, then the length of arc AXB is
Read the following SAT test question and then click on a button to select your answer.
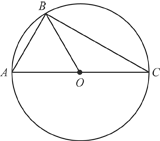
4.In the figure above, O is the center of the circle and triangle A B O is equilateral. If the sides of triangle A B O are of length 6, what is the length of line B C?
(A) 3 times square root 3
(B) 4 times square root 3
(C) 6 times square root 3
(D) 9
(E) 12

4.The correct answer is C
Choice (C) is correct. Since triangle A B O is equilateral, each of its angles has measure
60 degrees. It follows that angle B O C has measure 120 degrees. Since line O B and line O C are radii of the same circle, they are of equal length, and so delta O C B is isosceles. Hence angle O B C and angle O C B each have measure 30 degrees. Thus angle A B C has measure 60 degrees + 30 degrees = 90 degrees, and so triangle A B C is a 30 degrees minus 60 degrees minus 90 degrees right triangle. Since line A B, the side opposite the 30 degrees angle in triangle A B C, is of length 6, it follows that line B C, the side opposite the 60 degrees angle, is of length 6 times square root 3
以上就是這8道SAT數學練習題及答案的詳細內容,包括了一些常見的知識點。大家可以在備考的時候,對此加以適當的練習和應用,測試自己在數學方面知識點的掌握情況,以便及時調整自己的備考方案,提高備考的效率。











